
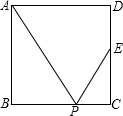
 如图所示,四边形ABCD是正方形,E是CD的中点,P是BC边上的一点,下列条件:①∠APB=∠EPC;②∠APE=∠APB;③P是BC的中点;④BP:BC=2:3,其中能推出△ABP∽△ECP的有( )
如图所示,四边形ABCD是正方形,E是CD的中点,P是BC边上的一点,下列条件:①∠APB=∠EPC;②∠APE=∠APB;③P是BC的中点;④BP:BC=2:3,其中能推出△ABP∽△ECP的有( )| A. | 1个 | B. | 2个 | C. | 3个 | D. | 4个 |
分析 利用相似三角形的判定定理,以及正方形的性质逐项判断即可.
解答 解:∵四边形ABCD为正方形,
∴AB=BC=CD,∠B=∠C=90°,
∵E为CD中点,
∴CD=2CE,即AB=BC=2CE,
①当∠APB=∠EPC时,结合∠B=∠C,可推出△ABP∽△ECP;
②当∠APE=∠APB≠60°时,则有∠APB≠∠EPC,所以不能推出△ABP∽△ECP;
③当P是BC中点时,则有BC=2PC,可知PC=CE,则△PCE为等腰直角三角形,而BP≠AB,即△ABP不是等腰直角三角形,故不能推出△ABP∽△ECP;④当BP:BC=2:3时,则有BP:PC=2:1,且AB:CE=2:1,结合∠B=∠C,可推出△ABP∽△ECP相似;
故选B.
点评 本题考查了相似三角形的判定定理:(1)两角对应相等的两个三角形相似.(2)两边对应成比例且夹角相等的两个三角形相似.(3)三边对应成比例的两个三角形相似.(4)如果一个直角三角形的斜边和一条直角边与另一个直角三角形的斜边和一条直角边对应成比例,那么这两个直角三角形相似.也考查了正方形的性质.


科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
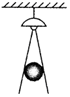 如图,在一间黑屋子里用一盏白炽灯照一个球,球在地面上的阴影的形状是一个圆,当把球向远离灯的位置移动时,圆形阴影面积的大小的变化情况是变小.
如图,在一间黑屋子里用一盏白炽灯照一个球,球在地面上的阴影的形状是一个圆,当把球向远离灯的位置移动时,圆形阴影面积的大小的变化情况是变小.查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 1 | B. | 5 | C. | 1或5 | D. | 无法计算 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
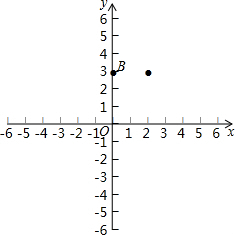 已知抛物线y=ax2+bx+c的顶点为A,经过点B(0,3)和点(2,3),与x轴交于C,D两点,(点C在点D的左侧),且OD=OB.
已知抛物线y=ax2+bx+c的顶点为A,经过点B(0,3)和点(2,3),与x轴交于C,D两点,(点C在点D的左侧),且OD=OB.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com