
 我国是世界上严重缺水的国家之一.为了增强居民的节水意识,某市自来水公司对居民用水采用以户为单位分段计费的办法收费.即一个月用水10吨以内(包括10吨)的用户,每吨收水费a元;一个月用水超过10吨的用户,10吨水仍按每吨a元收费,超过10吨的部分,按每吨b元(b>a)收费.设一户居民月用水x吨,应收水费y元,y与x之间的函数关系如图:
我国是世界上严重缺水的国家之一.为了增强居民的节水意识,某市自来水公司对居民用水采用以户为单位分段计费的办法收费.即一个月用水10吨以内(包括10吨)的用户,每吨收水费a元;一个月用水超过10吨的用户,10吨水仍按每吨a元收费,超过10吨的部分,按每吨b元(b>a)收费.设一户居民月用水x吨,应收水费y元,y与x之间的函数关系如图:分析 (1)根据题意和函数图象可以求得a的值;
(2)根据题意和函数图象中的数据可以求得b的值,并求出当x≥10时,y与x之间的函数关系式.
解答 解:(1)由题意可得,
a=15÷10=1.5,
用8吨水应收水费:8×1.5=12(元),
答:a的值是1.5,一个月用水8吨时的水费是12元;
(2)由题意可得,
b=(35-15)÷(20-10)=20÷10-2,
设当x≥10时,y与x的函数关系式为y=kx+m,
$\left\{\begin{array}{l}{10k+m=15}\\{20k+m=35}\end{array}\right.$,得$\left\{\begin{array}{l}{k=2}\\{m=-5}\end{array}\right.$,
即当x≥10时,y与x的函数关系式为y=2x-5,
答:b的值是2,当x≥10时,y与x的函数关系式为y=2x-5.
点评 本题考查一次函数的应用,解答本题的关键是明确题意,求出相应的函数解析式,利用数形结合的思想解答.


科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
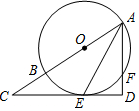 如图,AB是⊙O的直径,AE平分∠BAF,交⊙O于点E,过点E作直线ED⊥AF,交AF的延长线于点D,交AB的延长线于点C.
如图,AB是⊙O的直径,AE平分∠BAF,交⊙O于点E,过点E作直线ED⊥AF,交AF的延长线于点D,交AB的延长线于点C.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
| 序号 | 1 | 2 | 3 | … |
| 图形 |  |  |  | … |
| ●的个数 | 8 | 16 | 24 | … |
| ★的个数 | 1 | 4 | 9 | … |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com