
【题目】如图,在 Rt△ABC 中,∠BAC=90°,∠BAC 的平分线交 BC 于点 O,以 O 为圆心作圆,⊙O 与 AC 相切于点 D.
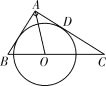
(1)试判断 AB 与⊙O 的位置关系,并加以证明;
(2)在 Rt△ABC 中,若 AC=6,AB=3,求切线 AD 的长.
【答案】(1)BA与⊙O相切,证明见解析;(2)AD的长为2.
【解析】
(1)过点O作OE⊥AB,垂足为E,连接OD,根据角平分线性质得出OE=OD,据此进一步证明即可.
(2)设⊙O的半径为r,根据△ABC面积=△AOC面积+△BOA面积进一步分析得出⊙O半径,然后通过证明AD=OD求出长度即可.
(1)
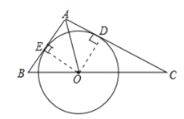
如图,过点O作OE⊥AB,垂足为E,连接OD,
∵AC是圆的切线,
∴OD⊥AC,
∵OA为∠BAC的角平分线,OE⊥AB,
∴OE=OD,
即OE是该圆的半径,
∴BA与⊙O相切;
(2)设⊙O的半径为r,
∵△ABC面积=△AOC面积+△BOA面积,
∴![]() ,
,
∵OE=OD=r,AC=6,AB=3,
∴![]() ,
,
即:![]() ,
,
∴![]() ,
,
∵OA为∠BAC的角平分线,
∴∠OAD=45°,
∵OD⊥AC,
∴∠AOD=45°,
∴AD=OD=r,
即AD的长为2.


科目:初中数学 来源: 题型:
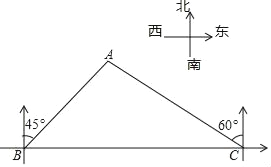
【题目】如图,一位旅行者骑自行车沿湖边正东方向笔直的公路BC行驶,在B地测得湖中小岛上某建筑物A在北偏东45°方向,行驶12min后到达C地,测得建筑物A在北偏西60°方向如果此旅行者的速度为10km/h,求建筑物A到公路BC的距离.(结果保留根号)
查看答案和解析>>
科目:初中数学 来源: 题型:
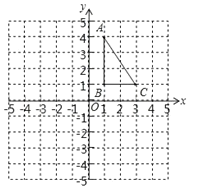
【题目】如图,在平面直角坐标系中,△ABC的三个顶点的坐标分别为A(1,4),B(1,1),C(3,1).
(1)画出△ABC关于原点成中心对称的△A1B1C1,并写出点C1的坐标;
(2)△ABC绕着点B逆时针旋转90°,画出旋转后对应的△A2BC2,并写出点A2的坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】将抛物线y=﹣x2向左平移3个单位,再向上平移4个单位.
(1)写出平移后的抛物线的函数关系式.
(2)若平移后的抛物线的顶点为A,与x轴的两个交点分别是B、C,求△ABC的面积.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】(2016广西贺州市)如图,将线段AB绕点O顺时针旋转90°得到线段A′B′,那么A(﹣2,5)的对应点A′的坐标是( )

A. (2,5) B. (5,2) C. (2,﹣5) D. (5,﹣2)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在Rt△ABC中,∠ACB=90°,∠BAC=α,点D在边AC上(不与点A,C重合)连接BD,点K为线段BD的中点,过点D作DE⊥AB于点E,连结CK,EK,CE,将△ADE绕点A顺时针旋转一定的角度(旋转角小于90°)

(1)如图1,若α=45°,则△ECK的形状为______;
(2)在(1)的条件下,若将图1中的△ADE绕点A旋转,使得D,E,B三点共线,点K为线段BD的中点,如图2所示,求证:BE-AE=2CK;
(3)若△ADE绕点A旋转至图3位置时,使得D,E,B三点共线,点K仍为线段BD的中点,请你直接写出BE,AE,CK三者之间的数量关系(用含α的三角函数表示).
查看答案和解析>>
科目:初中数学 来源: 题型:
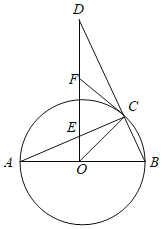
【题目】如图,AB是⊙O的直径,C是⊙O上一点,过点O作OD⊥AB,交BC的延长线于D,交AC于点E,F是DE的中点,连接CF.
(1)求证:CF是⊙O的切线.
(2)若∠A=22.5°,求证:CE=CB.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com