(1)证明:∵A
0F、A
0C都是圆的切线,
∴A
0F=A
0C,
又∵A
0F=A
0D,∴A
0C=A
0D;
∵∠DA
0E=∠CA
0B,∠EDA
0=∠BCA
0=90°,
∴△A
0DE≌△A
0CB.
(2)解:连接CM,则CM⊥A
1B;
∵A
1F=A
1D,且A
1F:A
1E=1:2,
∴A
1D:A
1E=1:2,即∠MA
1C=60°,∠A
1CM=30°;
设A
1C=

x,则CM=

x,BC=

x;
在Rt△BCM中,BC:CM=

x:

x=

:1,
∴∠BCM=45°,
∴∠BCA
1=∠BCM+∠A
1CM=75°.
(3)解:①当AE与圆相切时,由(1)可知:△ADE≌△ACB,
此时S
△ADE=S
△ABC;
②当AE与圆相交时,设AE与圆的另一个交点为N,连接BN,CM;
由CM∥DE可得:CM:DE=AM:AD=AM:AF,
由切线长定理:AF
2=AM×AB,
得:AM:AF=AF:AB,
∴CM:DE=AF:AB,
∴AF•DE=AB•MC,
∴AD•DE=AB•MC,
∴

AD•DE=

AB•MC=S
△ABC,
由于A点在平行于AB的直线上运动,因此△ABC的面积为定值,且S
△ABC=

×4×3=6;
故△ADE的面积S与A的位置无关,且恒为6.
分析:(1)由于A
0F、A
0C都是圆的切线,由切线长定理知:A
0F=A
0C,由此可得A
0D=A
0C,再加上公共角∠BA
0E、一组直角,即可证得所求的三角形全等.
(2)连接CM,则CM⊥A
1B,已知A
1F:A
1E=1:2,即A
1D:A
1E=1:2,由此可求得∠DA
1E=60°,∠A
1CM=30°;首先用未知数表示出A
1C、BC的长,在Rt△A
1CM中,根据∠MA
1C的度数可表示出CM的值,进而可在Rt△BCM中,根据CM、BC的值求出∠BCM的度数,由此得解.
(3)此题应分两种情况讨论:
①如图2的情况,即AE与圆相切,此时△ABC≌△ADE,因此△ADE的面积等于△ABC的面积;
②如图1、3的情况,即AE与圆相交,设AE与圆的另一个交点为N,连接BN、CM,由CM∥DE可得:CM:DE=AM:AD=AM:AF,
由切线长定理:AF
2=AM×AB,由于A点在直线PQ上运动,所以△ABC的面积是不变的,因此△ADE的面积也不变,即S与A的位置无关.
点评:此题主要考查了切线的性质、相似三角形以及全等三角形的判定和性质、三角形面积的计算方法等知识,难度较大.

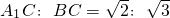 .求角BCA1的大小;
.求角BCA1的大小;
 x,则CM=
x,则CM= x,BC=
x,BC= x;
x; x:
x: x=
x= :1,
:1, AD•DE=
AD•DE= AB•MC=S△ABC,
AB•MC=S△ABC, ×4×3=6;
×4×3=6;

 小学学习好帮手系列答案
小学学习好帮手系列答案 小学同步三练核心密卷系列答案
小学同步三练核心密卷系列答案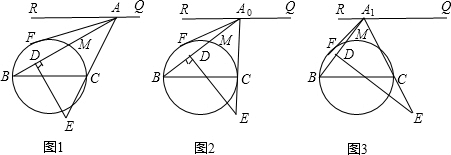
 .求角BCA1的大小;
.求角BCA1的大小;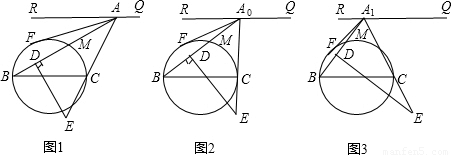
 .求角BCA1的大小;
.求角BCA1的大小;
 .求角BCA1的大小;
.求角BCA1的大小;