
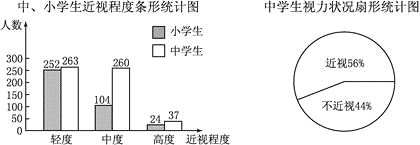
【题目】某市青少年健康研究中心随机抽取了本市1000名小学生和若干名中学生,对他们的视力状况进行了调查,并把调查结果绘制成如下统计图.(近视程度分为轻度、中度、高度三种)
(1)求这1000名小学生患近视的百分比.
(2)求本次抽查的中学生人数.
(3)该市有中学生8万人,小学生10万人.分别估计该市的中学生与小学生患“中度近视”的人数.
【答案】(1)这1000名小学生患近视的百分比为38%. (2)本次抽查的中学生有1000人. (3)该市中学生患“中度近视”的约有2.08万人,患“中度近视”的约有1.04万人.
【解析】
(1)这1000名小学生患近视的百分比=小学生近视的人数÷总人数×100﹪
(2)调查中学生总人数=中学生近视的人数÷中学生患近视的百分比
(3)用样本估计总体,该市中学生患“中度近视”的人数=8万×1000名中学生患中度近视的百分比;该市小学生患“中度近视”的人数=10万×1000名小学生患中度近视的百分比
解:(1)∵(252+104+24)÷1000=38%,
∴这1000名小学生患近视的百分比为38%.
(2)∵(263+260+37)÷56%=1000(人),
∴本次抽查的中学生有1000人.
(3)∵8×![]() =2.08(万人),
=2.08(万人),
∴该市中学生患“中度近视”的约有2.08万人.
∵10×![]() =1.04(万人),
=1.04(万人),
∴该市小学生患“中度近视”的约有1.04万人.


科目:初中数学 来源: 题型:
【题目】已知直线l经过A(6,0)和B(0,12)两点,且与直线y=x交于点C,点P(m,0)在x轴上运动.
(1)求直线l的解析式;
(2)过点P作l的平行线交直线y=x于点D,当m=3时,求△PCD的面积;
(3)是否存在点P,使得△PCA成为等腰三角形?若存在,请直接写出所有符合条件的点P的坐标;若不存在,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
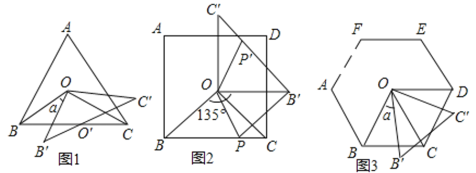
【题目】在下列正多边形中,![]() 是中心,定义:
是中心,定义:![]() 为相应正多边形的基本三角形.如图1,
为相应正多边形的基本三角形.如图1,![]() 是正三角形
是正三角形![]() 的基本三角形;如图2,
的基本三角形;如图2,![]() 是正方形
是正方形![]() 的基本三角形;如图3,
的基本三角形;如图3,![]() 为正
为正![]() 边形
边形![]() …的基本三角形.将基本
…的基本三角形.将基本![]() 绕点
绕点![]() 逆时针旋转
逆时针旋转![]() 角度得
角度得![]() .
.
(1)若线段![]() 与线段
与线段![]() 相交点
相交点![]() ,则:
,则:
图1中![]() 的取值范围是________;
的取值范围是________;
图3中![]() 的取值范围是________;
的取值范围是________;
(2)在图1中,求证![]()
(3)在图2中,正方形边长为4,![]() ,边
,边![]() 上的一点
上的一点![]() 旋转后的对应点为
旋转后的对应点为![]() ,若
,若![]() 有最小值时,求出该最小值及此时
有最小值时,求出该最小值及此时![]() 的长度;
的长度;
(4)如图3,当![]() 时,直接写出
时,直接写出![]() 的值.
的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】问题探究:
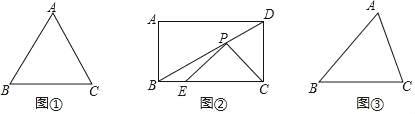
(1)如图①,已知等边△ABC,边长为4,则△ABC的外接圆的半径长为 .
(2)如图②,在矩形ABCD中,AB=4,对角线BD与边BC的夹角为30°,点E在为边BC上且BE=![]() BC,点P是对角线BD上的一个动点,连接PE,PC,求△PEC周长的最小值.
BC,点P是对角线BD上的一个动点,连接PE,PC,求△PEC周长的最小值.
问题解决:
(3)为了迎接新年的到来,西安城墙举办了迎新年大型灯光秀表演.其中一个镭射灯距城墙30米,镭射灯发出的两根彩色光线夹角为60°,如图③,若将两根光线(AB,AC)和光线与城墙的两交点的连接的线段(BC)看作一个三角形,记为△ABC,那么该三角形周长有没有最小值?若有,求出最小值,若没有,说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图①,在四边形ABCD中,AB∥CD,∠B=90°,AB=2CD.动点P从点A出发,在四边形ABCD的边上沿A→B→C的方向以1cm/s的速度匀速移动,到达点C时停止移动。已知△APD的面积S(cm 2)与点P运动的时间t(s)之间的函数图象如图②所示,根据题意解答下列问题
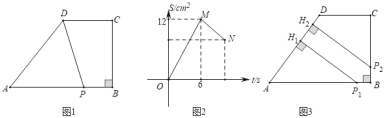
(1)在图①中,AB= cm, BC= cm.
(2)求图2中线段MN的函数关系式(并写出t的取值范围) .
(3)如图③,设动点P用了t1 (s)到达点P1处,用了t2 (s)到达点P2处,分别过P1、P2作AD的垂线,垂足为H1、H2.当P1H1= P2H2=4时,连P1P2,求△BP1P2的面积.
查看答案和解析>>
科目:初中数学 来源: 题型:
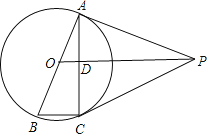
【题目】如图,AB是⊙O的直径,AC是弦,OD⊥AC于点D,过点A作⊙O的切线AP,AP与OD的延长线交于点P,连接PC、BC.
【1】猜想:线段OD与BC有何数量和位置关系,并证明你的结论.
【2】求证:PC是⊙O的切线
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】中国“蛟龙”号深潜器目前最大深潜极限为7062.68米.某天该深潜器在海面下1800米处作业(如图),测得正前方海底沉船C的俯角为45°,该深潜器在同一深度向正前方直线航行2000米到B点,此时测得海底沉船C的俯角为60°.请判断沉船C是否在“蛟龙”号深潜极限范围内?并说明理由;(精确到0.01)(参考数据:![]() ≈1.414,
≈1.414,![]() ≈1.732)
≈1.732)

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知四边形ABCD是平行四边形,AD=BD,过点D作DE⊥AB于点E,过点A作AH⊥BD于点H,交DE、BC分别于点F、G,连接CF.

(1)如图1,求证:∠BAG=∠FCB;
(2)如图2,过点A作AK平分∠DAF交ED于点K,若AK=1,∠FCD=45°,求DF的长;
(3)如图3,若AD=10,DH=6,求CF的长.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com