
| A. | $\frac{a}{b}$ | B. | $\frac{{a}^{2}}{b}$ | C. | $\frac{b}{a}$ | D. | $\frac{{b}^{2}}{a}$ |
分析 设锅炉的高h,底面直径d,根据圆柱的表面积计算公式列出函数关系式,然后求其最值.
解答 解:设锅炉的高h与底面直径d的比是$\frac{h}{d}$=k,
${∵(\frac{d}{2})}^{2}π•h=v=\frac{{πd}^{2}}{4}•kd={\frac{πk}{4}d}^{3}$,
∴$d=\root{3}{\frac{4v}{πk}}$,h=kd=$\root{3}{\frac{4{vk}^{2}}{π}}$,
设造价为y,则y=2π${•(\frac{d}{2})}^{2}$•a+πd•h•b=$\frac{πa}{2}$$•\root{3}{\frac{1{6v}^{2}}{{π}^{2}}}{•k}^{-\frac{2}{3}}$+πb$•\root{3}{\frac{1{6v}^{2}}{{π}^{2}}}$${•k}^{\frac{1}{3}}$,
∴y′=$\frac{πa}{2}$$\root{3}{\frac{1{6v}^{2}}{{π}^{2}}}$$•(-\frac{2}{3})$${k}^{-\frac{5}{3}}$+πb$\root{3}{\frac{1{6v}^{2}}{{π}^{2}}}$$\frac{1}{3}$${k}^{-\frac{2}{3}}$,
令y′=0,k=$\frac{a}{b}$时,y=ymin,
∴当造价最低时,锅炉的高与底面直径的比是$\frac{a}{b}$,
故选A.
点评 本题考查了函数在实际问题中的应用,熟记公式是解题的关键.


 孟建平小学滚动测试系列答案
孟建平小学滚动测试系列答案科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 如图,在△ABC中,O是BC上的点,⊙O经过A,B两点,与BC交于点E,D是下半圆的点,且OD⊥BC于点O,并连结AD交BC于点F,若AC是⊙O的切线.
如图,在△ABC中,O是BC上的点,⊙O经过A,B两点,与BC交于点E,D是下半圆的点,且OD⊥BC于点O,并连结AD交BC于点F,若AC是⊙O的切线.查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
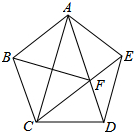 如图,在正五边形ABCDE中,连接AC、AD、CE,CE交AD于点F,连接BF,已知AB=1,则DF的长是( )
如图,在正五边形ABCDE中,连接AC、AD、CE,CE交AD于点F,连接BF,已知AB=1,则DF的长是( )| A. | $\frac{\sqrt{5}+1}{2}$ | B. | $\frac{1}{2}$ | C. | $\frac{\sqrt{5}}{2}$ | D. | $\frac{\sqrt{5}-1}{2}$ |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com