练习册

  • 练习册
  • 试题
    精英家教网 > 初中数学 > 题目详情
    10．菱形的一个内角是120°，一条较短的对角线的长为10，则菱形的周长是（　　）
    A．10B．20C．30D．40

    分析 首先根据题意画出图形，然后由菱形的一个内角是120°，证得△ABD是等边三角形，继而可得边长等于较短的对角线的长，则可求得答案．

    解答 解：如图，∵菱形ABCD中，∠ABC=120°，
    ∴AB=AD，∠A=60°，
    ∴△ABD是等边三角形，
    ∴AB=BD=10，
    ∴菱形的周长是：40．
    故选D．

    点评 此题考查了菱形的性质以及等边三角形的判定与性质．注意证得△ABD是等边三角形是关键．

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：初中数学 来源： 题型：解答题

    20．为了解某校八年级学生每天干家务活的平均时间，小颖同学在该校八年级每班随机调查5名学生，统计这些学生2015年3月每天干家务活的平均时间（单位：min），绘制成如下统计表（其中A表示0～10min；B表示11～20min；C表示21～30min，时间取整数）：
     干家务活平均时间 频数 百分比
     A 10 25%
     B a 62.5%
     C 5 b
     合计 c1 
    （1）统计表中的a=25；b=12.5%；c=40．
    （2）从上表的“频数”、“百分比”两列数据中选择一列，用适当的统计图表示．
    （3）该校八年级共有240学生，求每天干家务活的平均时间在11～20min的学生人数．

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

    1．已知a为有理数，化简：$\sqrt{-{a}^{3}}$-a$\sqrt{-\frac{1}{a}}$．

    查看答案和解析>>

    科目：初中数学 来源： 题型：选择题

    18．下列三条线段能构成直角三角形的是（　　）
    A．4，5，6B．1，2，3C．3，6，9D．6，8，10

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

    5．如图，某港口P位于东西方向的海岸线上“远航”号、“海天”号轮船同时离开港口，各自沿同定方向航行，“远航”号每小时航行16n mile，“海天”号每小时航行12n mile，它们离开港口一个半小时后分别位于点Q，R处，且相距30n mile
    （1）求PQ，PR的长度；
    （2）如果知道“远航”号沿东北方向航行，能知道“海天”号沿哪个方向航行吗？

    查看答案和解析>>

    科目：初中数学 来源： 题型：填空题

    15．把正整数1，2，3，…，按如图所示排列．第1行第1列的数为1，第1行第2列的数为2，第1行第3列的数为6，那么第1行第100列的数为4951．

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

    1．已知：抛物线y=mx2+（2m+2）x+m+2与x轴交于点A、B （A左B右），其中点B的坐标为（7，0），设抛物线的顶点为C．

    （1）求抛物线的解析式和点C的坐标；
    （2）如图1，若AC交y轴于点D，过D点作DE∥AB交BC于E．点P为DE上一动点，PF⊥AC于F，PG⊥BC于G．设点P的横坐标为a，四边形CFPG的面积为y，求y与a的函数关系式和y的最大值；
    （3）如图2，在条件（2）下，过P作PH⊥x轴于点H，连结FH、GH，是否存在点P，使得△PFH与PHG相似？若存在，求出P点坐标；若不存在，说明理由．

    查看答案和解析>>

    科目：初中数学 来源： 题型：选择题

    18．如图，正方形ABCD中，E为AB的中点，AF⊥DE于点O，则$\frac{OE}{BF}$等于（　　）
    A．$\frac{1}{2}$B．$\frac{1}{3}$C．$\frac{\sqrt{5}}{5}$D．$\frac{2\sqrt{5}}{3}$

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

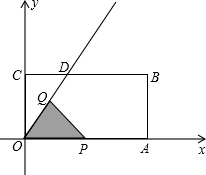    19．如图，已知矩形ABCD中，OA=8，AB=1，直线y=$\frac{4}{3}$x交BC于D，动点P、Q同时从D出发，点P沿折线OA-AB-BD以每秒3个单位的速度运动到D停止，点Q沿射线OD以每秒1个单位的速度运动，当点P停止时，点Q也停止运动．△OPQ与梯形OABD重叠部分的面积为S，运动时间为t．
    （1）求D的坐标；
    （2）写出面积S与时间t的函数关系式；
    （3）t为何值时，S有最大值，并求出最大值．

    查看答案和解析>>

    同步练习册答案