
分析 (1)本题的等量关系是:两种电视的台数和=50台,买两种电视花去的费用=9万元.然后分进的两种电视是A、B,A、C,B、C三种情况进行讨论.求出正确的方案;
(2)根据(1)得出的方案,分别计算出各方案的利润,然后判断出获利最多的方案.
解答 解:按购A,B两种,B,C两种,A,C两种电视机这三种方案分别计算,设购A种电视机x台,则B种电视机y台.
①当选购A,B两种电视机时,B种电视机购(50-x)台,可得方程:
1500x+2100(50-x)=90000,即5x+7(50-x)=300,
解得:x=25,
则B种电视机购50-25=25(台);
②当选购A,C两种电视机时,C种电视机购(50-x)台,可得方程:
1500x+2500(50-x)=90000,
解得:x=35,
则C种电视机购50-35=15(台);
③当购B,C两种电视机时,C种电视机为(50-y)台,可得方程:
2100y+2500(50-y)=90000,
解得:y=$\frac{175}{2}$,(不合题意,舍去)
由此可选择两种方案:一是购A,B两种电视机25台;二是购A种电视机35台,C种电视机15台.
(2)若选择(1)中的方案①,可获利150×25+250×15=8750(元),
若选择(1)中的方案②,可获利150×35+250×15=9000(元),
因为9000>8750,
所以为了获利最多,选择第二种方案.
点评 此题考查了一元一次方程的应用.解题关键是要读懂题目的意思,根据题目给出的条件,找出合适的等量关系:两种电视的台数和=50台,买两种电视花去的费用=9万元.列出方程,再求解.


科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
 如图,四边形ABCD为矩形,点E在AD边上,DE=4AE,EF∥AC,交CD边于点F,连接BE,若∠DEF=2∠ABE,BE=2$\sqrt{3}$,则线段EF的长为$\frac{24}{5}$.
如图,四边形ABCD为矩形,点E在AD边上,DE=4AE,EF∥AC,交CD边于点F,连接BE,若∠DEF=2∠ABE,BE=2$\sqrt{3}$,则线段EF的长为$\frac{24}{5}$.查看答案和解析>>
科目:初中数学 来源: 题型:选择题
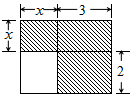 下面四个整式中,不能表示图中阴影部分面积的是( )
下面四个整式中,不能表示图中阴影部分面积的是( )| A. | (x+3)(x+2)-2x | B. | x(x+3)+6 | C. | 3(x+2)+x2 | D. | x2+5x |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 了解一批圆珠笔的使用寿命 | |
| B. | 了解全国八年级学生身高的现状 | |
| C. | 检查发射神舟11号飞船的运载火箭的各零部件 | |
| D. | 考察世界人们保护海洋的意识 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题

查看答案和解析>>
科目:初中数学 来源: 题型:解答题

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com