
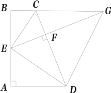
【题目】如图,已知四边形ABCD中,AB⊥AD,BC∥AD,E为AB的中点,且EC、ED分别为∠BCD、∠ADC的角平分线,EF⊥CD交BC的延长线于点G,连接DG.
(1)求证:CE⊥DE;
(2)若AB=6,求CF·DF的值;
(3)当△BCE与△DFG相似时,![]() 的值是 .
的值是 .
【答案】(1)证明见解析;(2)CF·DF的值为9;(3)![]() 的值为
的值为![]() 或
或![]()
【解析】
(1)利用平行线及角平分线的性质即可证明;
(2)可证△CFE∽△EFD,可得![]() ,变形得
,变形得![]() 由角平分线性质可得
由角平分线性质可得
FF=EA=3,代入即可得结论
(3)分类讨论:若△BCE∽△FDG,可证△BCE≌△FEC、△ADE≌△FED,过G作GH⊥AD于H可证△BCE∽△HDG可得![]() 即可得
即可得![]() ;当△BCD∽△FGD时可证△CFE≌△CFG可推出∠1=60°,∠4=30°在Rt△BCE中
;当△BCD∽△FGD时可证△CFE≌△CFG可推出∠1=60°,∠4=30°在Rt△BCE中 ![]() ,在Rt△ADE中
,在Rt△ADE中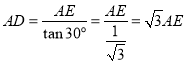 即可得
即可得![]() 的值.
的值.
(1)证明:
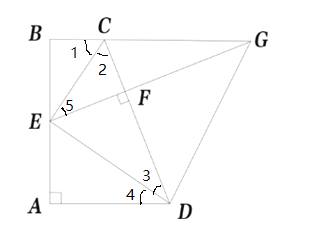
∵BC∥AD
∴∠BCD+∠ADC=180°
∵EC、ED分别平分∠BCD、∠ADC
∴∠1=∠2,∠3=∠4,∠1+∠2+∠3+∠4=180°
∴∠2+∠3=90° ∴∠CED=90°
∴CE⊥DE
(2)∵CE⊥DE,EF⊥CD
∴∠2+∠5=90°,∠2+∠3=90°
∴∠5=∠3
∴△CFE∽△EFD
∴![]()
∴![]()
∵ED平分∠FDA,∠A=∠EFD=90°
∴FF=EA
∵E为AB中点,AB=6
∴FE=AE=BE=3
∴![]()
(3) 若△BCE∽△FDG
∴∠1=∠FDG
∵∠1=∠2
∴∠2=∠FDG
∴EC∥CD
∴![]()
∵∠1=∠2,∠EBC=∠CFE=90°,EC=EC
∴△BCE≌△FCE
∴BC=CF
∵∠3=∠4,∠A=∠EFD=90°,ED=ED
∴△ADE≌△FDE
∴AD=FD
∴![]()
∴![]()
过G作GH⊥AD于H
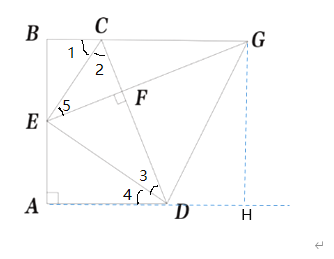
∴∠DHG=90°
∵∠3=∠4,∠FDG=∠2
又∵∠3+∠4+∠FDG+∠GDH=180°
∠3+∠4+∠1+∠2=180°
∴∠GDH=∠1
又∵∠GFD=∠B=90°
∴△BCE∽△HDG
∴![]()
∵![]()
∴![]()
∴![]()
∴![]()
∴![]()
当△BCD∽△FGD
∴∠GDF=∠BEC
∴∠BEC=∠5=∠3=∠4
∵FD=FD,∠3=∠FDG,∠EFD=∠GFD
∴△EDF≌△GFD
∴EF=FG
∵FD⊥EG
∴∠EFC=∠GFC=90°
又∵CF=CF
∴△CFE≌△CFG
∴∠2=∠GCD
∴∠1=∠2=∠GCD
∵∠1+∠2+∠GCD=180°
∴∠1=60°
∴∠4=30°
在Rt△BCE中 ![]()
在Rt△ADE中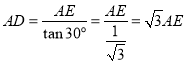
∴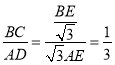
综上所述![]() 的值为
的值为![]() 或
或![]()


科目:初中数学 来源: 题型:
【题目】如图,在矩形![]() 中,
中,![]() ,
,![]() ,反比例函数
,反比例函数![]() (
(![]() )的图像与矩形两边AB、BC分别交于点D、点E,且
)的图像与矩形两边AB、BC分别交于点D、点E,且![]() .
.
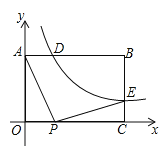
(1)求点D的坐标和![]() 的值;
的值;
(2)求证:![]() ;
;
(3)若点![]() 是线段
是线段![]() 上的一个动点,是否存在点
上的一个动点,是否存在点![]() ,使
,使![]() ?若存在,求出此时点
?若存在,求出此时点![]() 的坐标;若不存在,请说明理由.
的坐标;若不存在,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在△ABC中,∠C=90°,点O在AC上,以OA为半径的⊙O交AB于点D,BD的垂直平分线交BC于点E,交BD于点F,连接DE.
(1)判断直线DE与⊙O的位置关系,并说明理由;
(2)若AC=6,BC=8,OA=2,求线段DE的长.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】为了传承中华民族优秀传统文化,我市某中学举行“汉字听写”比赛,赛后整理参赛学生的成绩,将学生的成绩分为A,B,C,D四个等级,并将结果绘制成图1的条形统计图和图2扇形统计图,但均不完整.请你根据统计图解答下列问题:
(1)求参加比赛的学生共有多少名?并补全图1的条形统计图.
(2)在图2扇形统计图中,m的值为_____,表示“D等级”的扇形的圆心角为_____度;
(3)组委会决定从本次比赛获得A等级的学生中,选出2名去参加全市中学生“汉字听写”大赛.已知A等级学生中男生有1名,请用列表法或画树状图法求出所选2名学生恰好是一名男生和一名女生的概率.

查看答案和解析>>
科目:初中数学 来源: 题型:
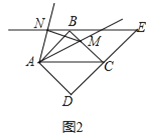
【题目】已知:如图①,将![]() 的菱形
的菱形![]() 沿对角线
沿对角线![]() 剪开,将
剪开,将![]() 沿射线
沿射线![]() 方向平移,得到
方向平移,得到![]() 点
点![]() 为边
为边![]() 上一点(点
上一点(点![]() 不与点
不与点![]() 、点
、点![]() 重合),将射线
重合),将射线![]() 绕点
绕点![]() 逆时针旋转
逆时针旋转![]() ,与
,与![]() 的延长线交于点
的延长线交于点![]() ,连接
,连接![]() .
.
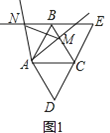
![]() ①求证:
①求证:![]() ;
;
②探究![]() 的形状;
的形状;
![]() 如图②,若菱形
如图②,若菱形![]() 变为正方形
变为正方形![]() ,将射线
,将射线![]() 绕点
绕点![]() 逆时针旋转
逆时针旋转![]() ,原题其他条件不变,
,原题其他条件不变,![]() 中的①和②两个结论是否仍然成立?若成立,请直接写出结论;若不成立,请写出变化后的结论并证明.
中的①和②两个结论是否仍然成立?若成立,请直接写出结论;若不成立,请写出变化后的结论并证明.
查看答案和解析>>
科目:初中数学 来源: 题型:
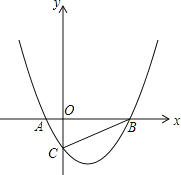
【题目】如图,在平面直角坐标系中,顶点为(![]() ,
,![]() )的抛物线交y轴于点C(0,﹣2),交x轴于点A,B(点A在点B的左侧).P点是y轴上一动点,Q点是抛物线上一动点.
)的抛物线交y轴于点C(0,﹣2),交x轴于点A,B(点A在点B的左侧).P点是y轴上一动点,Q点是抛物线上一动点.
(1)求抛物线的解析式;
(2)P点运动到何位置时,△POA与△ABC相似?并求出此时P点的坐标;
(3)当以A、B、P、Q四点为顶点的四边形为平行四边形时,求Q点的坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
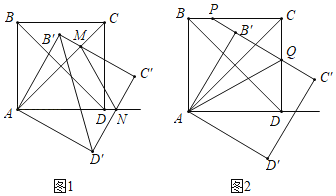
【题目】如图将正方形ABCD绕点A顺时针旋转角度α(0°<α<90°)得到正方形AB′C′D′.
(1)如图1,B′C′与AC交于点M,C′D′与AD所在直线交于点N,若MN∥B′D′,求α;
(2)如图2,C′B′与CD交于点Q,延长C′B′与BC交于点P,当α=30°时.
①求∠DAQ的度数;
②若AB=6,求PQ的长度.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com