
【题目】如图,二次函数y=ax2+bx+c的图象交x轴于A、B两点,交y轴于点C,且B(1,0),C(0,3),将△BOC绕点O按逆时针方向旋转90°,C点恰好与A重合.
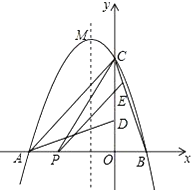
(1)求该二次函数的解析式;
(2)若点P为线段AB上的任一动点,过点P作PE∥AC,交BC于点E,连结CP,求△PCE面积S的最大值;
(3)设抛物线的顶点为M,Q为它的图象上的任一动点,若△OMQ为以OM为底的等腰三角形,求Q点的坐标.
【答案】(1)y=﹣x2﹣2x+3(2)![]() (3)Q(
(3)Q(![]() ,
,![]() ),或(
),或(![]() ,
,![]() )
)
【解析】试题分析:(1)根据题意求出A、B、C的坐标,然后根据待定系数法求函数的解析式即可;
(2)设点P(x,0),则PB=1﹣x,根据三角形的面积可得二次函数的解析式,然后根据二次函数的最值可求解;
(3)根据配方法求出顶点的坐标,然后根据等腰三角形的性质,结合勾股定理列方程可求解.
试题解析:(1)∵B(1,0),C(0,3),∴OB=1,OC=3.
∵△BOC绕点O按逆时针方向旋转90°,C点恰好与A重合.
∴OA=OC=3,∴A(﹣3,0),
∵点A,B,C在抛物线上,
∴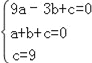 ,∴
,∴ ,∴二次函数的解析式为y=﹣x2﹣2x+3,
,∴二次函数的解析式为y=﹣x2﹣2x+3,
(2)设点P(x,0),则PB=1﹣x,
∴S△PBE=![]() (1﹣x)2,
(1﹣x)2,
∴S△PCE=S△PBC﹣S△PBE=![]() PB×OC﹣
PB×OC﹣![]() (1﹣x)2=
(1﹣x)2=![]() (1﹣x)×3﹣
(1﹣x)×3﹣![]() (1﹣x)2=﹣
(1﹣x)2=﹣![]() (x﹣1)2+
(x﹣1)2+![]() ,
,
当x=1时,S△PCE的最大值为![]() .
.
(3)∵二次函数的解析式为y=﹣x2﹣2x+3=﹣(x+1)2+4,
∴顶点坐标(﹣1,4),
∵△OMQ为等腰三角形,OM为底,
∴MQ=OQ,
∴![]() =
=![]() ,
,
∴8x2+18x=7=0,∴x=![]() ,∴y=
,∴y=![]() 或y=
或y=![]() ,
,
∴Q(![]() ,
,![]() ),或(
),或(![]() ,
,![]() ).
).


 优生乐园系列答案
优生乐园系列答案 新编小学单元自测题系列答案
新编小学单元自测题系列答案科目:初中数学 来源: 题型:
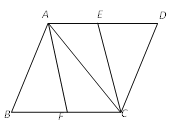
【题目】如图,在□ABCD中,E、F分别是AD、BC的中点,连接AC、CE、AF.
(1)求证△ABF ≌ △CDE;
(2)若AB=AC,求证四边形AFCE是矩形.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】阅读下面的材料:
如图①,在![]() 中,试说明
中,试说明![]() .
.
分析:通过画平行线,将![]() 、
、![]() 、
、![]() 作等量代换,使各角之和恰为一个平角,依辅助线不同而得多种方法.
作等量代换,使各角之和恰为一个平角,依辅助线不同而得多种方法.
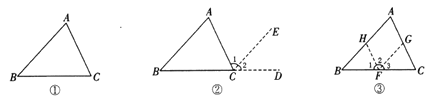
解:如图②,延长![]() 到点
到点![]() ,过点
,过点![]() 作
作![]() //
//![]() .
.
因为![]() //
//![]() (作图所知),
(作图所知),
所以![]() ,
,![]() (两直线平行,同位角、内错角相等).
(两直线平行,同位角、内错角相等).
又因为![]() (平角的定义),
(平角的定义),
所以![]() (等量代换).
(等量代换).
如图③,过![]() 上任一点
上任一点![]() ,作
,作![]() //
//![]() ,
, ![]() //
//![]() ,这种添加辅助线的方法能说
,这种添加辅助线的方法能说![]() 吗?并说明理由.
吗?并说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
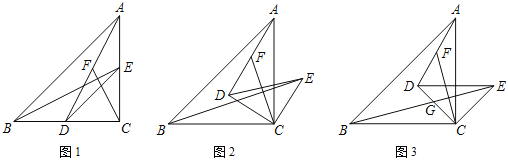
【题目】如图1,在Rt△ABC中,∠ACB=90°,AC=BC,D,E分别为AC,BC上的点,且CE=CD,连接DE,AD,BE,F为线段AD的中点,连接CF.
(1)求证:BE=2CF;
(2)如图2,把△DEC绕点C顺时针旋转α角(0°<α<90°),其他条件不变,试探究线段BE与CF的位置关系,并说明理由;
(3)如图3,把△DEC绕点C顺时针旋转45°,BE,CD交于点G.若∠DCF=30°,求![]() 及
及![]() 的值.
的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,等腰△ABC中,AB=AC,P为其底角平分线的交点,将△BCP沿CP折叠,使B点恰好落在AC边上的点D处,若DA=DP,则∠A的度数为( ) 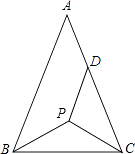
A.20°
B.30°
C.32°
D.36°
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】下面去括号正确的是( )
A. a﹣(b+1)=a﹣b﹣1B. 2(x+3)=2x+3
C. x﹣(y﹣1)=x﹣y﹣1D. ﹣3(m﹣n)=﹣3m﹣3n
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】二次函数y=ax2+bx+c(a≠0)的图象如图所示,下列结论正确的是( ) 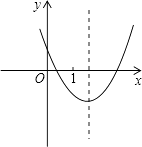
A.ac<0
B.当x=1时,y>0
C.方程ax2+bx+c=0(a≠0)有两个大于1的实数根
D.存在一个大于1的实数x0 , 使得当x<x0时,y随x的增大而减小;当x>x0时,y随x的增大而增大
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com