
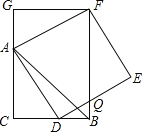
【题目】如图,已知![]() ,
,![]() ,点D在边BC上
,点D在边BC上![]() 与B,C不重合
与B,C不重合![]() ,四边形ADEF为正方形,过点F作
,四边形ADEF为正方形,过点F作![]() ,交CA的延长线于点G,连接FB,交DE于点Q,得出以下结论:
,交CA的延长线于点G,连接FB,交DE于点Q,得出以下结论:![]() ;
;![]() :2;
:2;![]() ;
;![]() 其中正确结论的个数是
其中正确结论的个数是![]()
![]()
A. 1 B. 2 C. 3 D. 4
【答案】D
【解析】分析:由正方形的性质得出∠FAD=90°,AD=AF=EF,证出∠CAD=∠AFG,由AAS证明△FGA≌△ACD,得出AC=FG,①正确;
证明四边形CBFG是矩形,得出S△FAB=![]() FBFG=
FBFG=![]() S四边形CBFG,②正确;
S四边形CBFG,②正确;
由等腰直角三角形的性质和矩形的性质得出∠ABC=∠ABF=45°,③正确;
证出△ACD∽△FEQ,得出对应边成比例,得出DFE=AD2=FQAC,④正确.
详解:∵四边形ADEF为正方形,
∴∠FAD=90°,AD=AF=EF,
∴∠CAD+∠FAG=90°,
∵FG⊥CA,
∴∠GAF+∠AFG=90°,
∴∠CAD=∠AFG,
在△FGA和△ACD中,
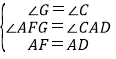 ,
,
∴△FGA≌△ACD(AAS),
∴AC=FG,故①正确;
∵BC=AC,
∴FG=BC,
∵∠ACB=90°,FG⊥CA,
∴FG∥BC,
∴四边形CBFG是矩形,
∴∠CBF=90°,S△FAB=![]() FBFG=
FBFG=![]() S四边形CBFG,故②正确;
S四边形CBFG,故②正确;
∵CA=CB,∠C=∠CBF=90°,
∴∠ABC=∠ABF=45°,故③正确;
∵∠FQE=∠DQB=∠ADC,∠E=∠C=90°,
∴△ACD∽△FEQ,
∴AC:AD=FE:FQ,
∴ADFE=AD2=FQAC,故④正确;
故选:D.


 开心试卷期末冲刺100分系列答案
开心试卷期末冲刺100分系列答案 双基同步导航训练系列答案
双基同步导航训练系列答案科目:初中数学 来源: 题型:
【题目】实验中学学生在学习等腰三角形性质“三线合一”时
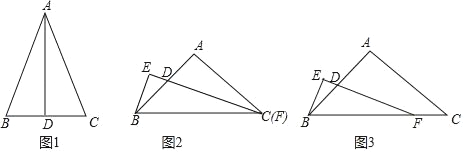
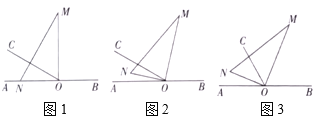
(1)(探究发现)如图1,在△ABC中,若AD平分∠BAC,AD⊥BC时,可以得出AB=AC,D为BC中点,请用所学知识证明此结论.
(2)(学以致用)如果Rt△BEF和等腰Rt△ABC有一个公共的顶点B,如图2,若顶点C与顶点F也重合,且∠BFE=![]() ∠ACB,试探究线段BE和FD的数量关系,并证明.
∠ACB,试探究线段BE和FD的数量关系,并证明.
(3)(拓展应用)如图3,若顶点C与顶点F不重合,但是∠BFE=![]() ∠ACB仍然成立,(学以致用)中的结论还成立吗?证明你的结论.
∠ACB仍然成立,(学以致用)中的结论还成立吗?证明你的结论.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,点C是AB的中点,点D是BC的中点,现给出下列等式:①CD=AC-DB,②CD=![]() AB,③CD=AD-BC,④BD=2AD-AB.其中正确的等式编号是( )
AB,③CD=AD-BC,④BD=2AD-AB.其中正确的等式编号是( )
![]()
A. ![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
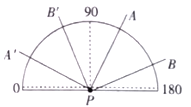
【题目】如图,把![]() 放置在量角器上,
放置在量角器上,![]() 与量角器的中心重合,读得射线
与量角器的中心重合,读得射线![]() 、
、![]() 分别经过刻度
分别经过刻度![]() 和
和![]() ,把
,把![]() 绕点
绕点![]() 逆时针方向旋转到
逆时针方向旋转到![]() ,下列结论:
,下列结论:
①![]() ;
;
②若射线![]() 经过刻度
经过刻度![]() ,则
,则![]() 与
与![]() 互补;
互补;
③若![]() ,则射线
,则射线![]() 经过刻度45.
经过刻度45.
其中正确的是( )
A.①②B.①③C.②③D.①②③
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图1,![]() 为直线
为直线![]() 上一点,过点
上一点,过点![]() 作射线
作射线![]() ,
,![]() ,将一直角三角板(
,将一直角三角板(![]() )的直角顶点放在点
)的直角顶点放在点![]() 处,一边
处,一边![]() 在射线
在射线![]() 上,另一边
上,另一边![]() 与
与![]() 都在直线
都在直线![]() 的上方.
的上方.
(1)将图1中的三角板绕点![]() 以每秒
以每秒![]() 的速度沿顺时针方向旋转一周.如图2,经过
的速度沿顺时针方向旋转一周.如图2,经过![]() 秒后,边
秒后,边![]() 恰好平分
恰好平分![]() .求
.求![]() 的值;
的值;
(2)在(1)问条件的基础上,若三角板在转动的同时,射线![]() 也绕
也绕![]() 点以每秒
点以每秒![]() 的速度沿顺时针方向旋转一周,如图3,那么经过多长时间
的速度沿顺时针方向旋转一周,如图3,那么经过多长时间![]() 平分
平分![]() ?请说明理由;
?请说明理由;
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,从左到右,在每个小格子中都填入一个整数,使得其中任意三个相邻格子中所填整数之和都相等.

(1)可求得x=___,第2009个格子中的数为___;
(2)判断:前m个格子中所填整数之和是否可能为2018?若能,求出m的值;若不能,请说明理由;
(3)如果a,b为前三个格子中的任意两个数,那么所有的|ab|的和可以通过计算|9&|+|9#|+|&#|+|&9|+|#9|+|#&|得到,若a,b为前19个格子中的任意两个数,则所有的|ab|的和为___.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】为了推动阳光体育运动的广泛开展,引导学生走向操场,积极参加体育锻炼,学校准备购买一批运动鞋供学生借用,现从各年级随机抽取了部分学生的鞋号,绘制了统计图①和图②,请根据相关信息,解答下列问题:
(1)本次接受随机抽样调查的学生人数为______,图①中![]() 的值为_____;
的值为_____;
(2)本次调查获取的样本数据的众数为______,中位数为________;
(3)根据样本数据,若学校计划购买200双运动鞋,建议购买35号运动鞋多少双?

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】下列说法正确的是
A. “明天降雨的概率是80%”表示明天有80%的时间都在降雨
B. “抛一枚硬币正面朝上的概率为![]() ”表示每抛2次就有一次正面朝上
”表示每抛2次就有一次正面朝上
C. “彩票中奖的概率为1%”表示买100张彩票肯定会中奖
D. “抛一枚正方体骰子,朝上的点数为2的概率为![]() ”表示随着抛掷次数的增加,“抛出朝上的点数为2”这一事件发生的频率稳定在
”表示随着抛掷次数的增加,“抛出朝上的点数为2”这一事件发生的频率稳定在![]() 附近
附近
查看答案和解析>>
科目:初中数学 来源: 题型:
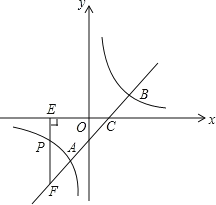
【题目】如图,直线![]() 与反比例函数
与反比例函数![]() 的图象交于
的图象交于![]() 、
、![]() 两点,与
两点,与![]() 轴交于点
轴交于点![]() ,已知点
,已知点![]() 的坐标为
的坐标为![]() .
.
(1)求反比例函数的解析式;
(2)若点![]() 是反比例函数图象上一点,过点
是反比例函数图象上一点,过点![]() 作
作![]() 轴于点
轴于点![]() ,延长
,延长![]() 交直线
交直线![]() 于点
于点![]() ,求
,求![]() 的面积.
的面积.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com