
°ĺŐ‚ńŅ°Ņ“—÷™Ň◊őÔŌŖy=ax2+bx+c”Žx÷ŠĹĽ”ŕA£®1£¨0£©£¨B£®3£¨0£©£¨”Žy÷ŠĹĽ”ŕC£®0£¨©Ā2£©£¨∂•Ķ„ő™D£¨Ķ„EĶń◊ÝĪÍő™£®0£¨©Ā1£©£¨ł√Ň◊őÔŌŖ”ŕBEĹĽ”ŕŃŪ“ĽĶ„F£¨Ń¨Ĺ”BC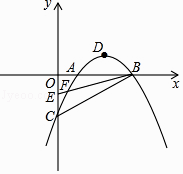
£®1£©«ůł√Ň◊őÔŌŖĶńĹ‚őŲ Ĺ£Ľ
£®2£©»ŰĶ„H£®1£¨y£©‘ŕBC…Ō£¨Ń¨Ĺ”FH£¨«ů°ųFHBĶń√śĽż£Ľ
£®3£©“Ľ∂ĮĶ„Mī”Ķ„D≥Ų∑Ę£¨“‘√Ņ√Ž1łŲĶ•őĽĶńňŔ∂»—ō∆Ĺ––”ŕy÷Š∑ĹŌÚŌÚ…Ō‘ň∂Į£¨Ń¨Ĺ”OM£¨BM£¨…Ť‘ň∂Į Īľšő™t√Ž£®t£ĺ0£©£¨Ķ„M‘ŕ‘ň∂ĮĻż≥Ő÷–£¨ĶĪtő™ļő÷Ķ Ī£¨°ŌOMB=90°„£Ņ
£®4£©‘ŕx÷Š…Ō∑ĹĶńŇ◊őÔŌŖ…Ō£¨ «∑Ůīś‘ŕĶ„P£¨ ĻĶ√°ŌPBFĪĽBA∆Ĺ∑÷£Ņ»Űīś‘ŕ£¨÷ĪĹ”–ī≥ŲĶ„PĶń◊ÝĪÍ£Ľ»Ű≤Ľīś‘ŕ£¨«ŽňĶ√ųņŻ”…£ģ
°ĺīūįł°Ņ
£®1£©
Ĺ‚£ļ…ŤŇ◊őÔŌŖĹ‚őŲ Ĺő™y=a£®x©Ā1£©£®x©Ā3£©£¨
į—C£®0£¨©Ā2£©īķ»ŽĶ√a£®©Ā1£©£®©Ā3£©=©Ā2£¨Ĺ‚Ķ√a=©Ā ![]() £¨
£¨
ňý“‘Ň◊őÔŌŖĹ‚őŲ Ĺő™y=©Ā ![]() £®x©Ā1£©£®x©Ā3£©£¨ľīy=©Ā
£®x©Ā1£©£®x©Ā3£©£¨ľīy=©Ā ![]() x2+
x2+ ![]() x©Ā2
x©Ā2
£®2£©
Ĺ‚£ļ…Ť÷ĪŌŖBEĶńĹ‚őŲ Ĺő™y=mx+n£¨
į—B£®3£¨0£©£¨E£®0£¨©Ā1£©īķ»ŽĶ√ ![]() £¨Ĺ‚Ķ√
£¨Ĺ‚Ķ√ 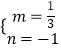 £¨
£¨
°ŗ÷ĪŌŖBEĶńĹ‚őŲ Ĺő™y= ![]() x©Ā1£¨
x©Ā1£¨
Õ¨—ý∑Ĺ∑®Ņ…«ůĶ√÷ĪŌŖBCĶńĹ‚őŲ Ĺő™y= ![]() x©Ā2£¨
x©Ā2£¨
Ĺ‚∑Ĺ≥Ő◊ť 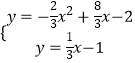 Ķ√
Ķ√ ![]() ĽÚ
ĽÚ 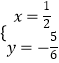 £¨‘ÚF£®
£¨‘ÚF£® ![]() £¨©Ā
£¨©Ā ![]() £©£Ľ
£©£Ľ
ĶĪx=1 Ī£¨y= ![]() ©Ā2=©Ā
©Ā2=©Ā ![]() £¨‘ÚH£®1£¨©Ā
£¨‘ÚH£®1£¨©Ā ![]() £©£¨
£©£¨
ѨŔAHĹĽBE”ŕQ£¨»ÁÕľ1£¨°ŖA£®1£¨0£©£¨H£®1£¨©Ā ![]() £©£¨
£©£¨
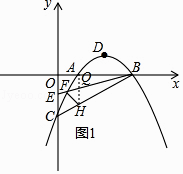
°ŗAH°Õx÷Š£¨
°ŗQ£®1£¨©Ā ![]() £©£¨
£©£¨
°ŗHQ=©Ā ![]() +
+ ![]() =
= ![]() £¨
£¨
°ŗS°ųFHB=S°ųBHQ+S°ųFHQ= ![]() °Ń
°Ń ![]() °Ń£®3©Ā
°Ń£®3©Ā ![]() £©
£© ![]()
£®3£©
Ĺ‚£ļĶĪx=2 Ī£¨y=©Ā ![]() x2+
x2+ ![]() x©Ā2=
x©Ā2= ![]() £¨‘ÚD£®2£¨
£¨‘ÚD£®2£¨ ![]() £©£¨
£©£¨
°ŗŇ◊őÔŌŖĶń∂‘≥∆÷Šő™÷ĪŌŖx=2£¨
÷ĪŌŖx=2ĹĽx÷Š”ŕN£¨»ÁÕľ2£¨MN=t+ ![]() £¨ON=2£¨BN=1£¨
£¨ON=2£¨BN=1£¨
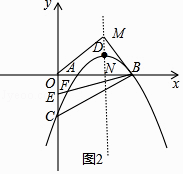
°Ŗ°ŌOMB=90°„£¨ľī°ŌOMN+°ŌBMN=90°„£¨
∂Ý°ŌOMN+°ŌMON=90°„£¨
°ŗ°ŌMON=°ŌBMN£¨
°ŗRt°ųOMN°◊Rt°ųMBN£¨
°ŗMN£ļBN=ON£ļMN£¨ľīMN2=BNON£¨
°ŗ£®t+ ![]() £©2=1°Ń2£¨Ĺ‚Ķ√t1=
£©2=1°Ń2£¨Ĺ‚Ķ√t1= ![]() ©Ā
©Ā ![]() £¨t2=©Ā
£¨t2=©Ā ![]() ©Ā
©Ā ![]() £®…Š»•£©£¨
£®…Š»•£©£¨
°ŗĶĪtő™ ![]() ©Ā
©Ā ![]() Ī£¨°ŌOMB=90°„£Ľ
Ī£¨°ŌOMB=90°„£Ľ
£®4£©
Ĺ‚£ļīś‘ŕ£ģ
»ÁÕľ3£¨BPĹĽy÷Š”ŕG£¨
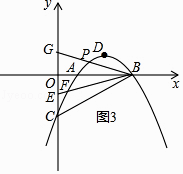
°ŖAB∆Ĺ∑÷°ŌFBP£¨
°ŗ°ŌGBO=°ŌEOB£¨
°ŗĶ„G”ŽĶ„EĻō”ŕx÷Š∂‘≥∆£¨
°ŗG£®0£¨1£©£¨
…Ť÷ĪŌŖBGĶńĹ‚őŲ Ĺő™y=px+q£¨
į—G£®0£¨1£©£¨B£®3£¨0£©īķ»ŽĶ√ ![]() £¨Ĺ‚Ķ√
£¨Ĺ‚Ķ√ 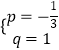 £¨
£¨
°ŗ÷ĪŌŖBQĶńĹ‚őŲ Ĺő™y=©Ā ![]() x+1£¨
x+1£¨
Ĺ‚∑Ĺ≥Ő◊ť 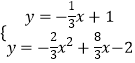 Ķ√
Ķ√ ![]() ĽÚ
ĽÚ ![]() £¨
£¨
°ŗPĶ„◊ÝĪÍő™£® ![]() £¨
£¨ ![]() £©£ģ
£©£ģ
°ĺĹ‚őŲ°Ņ£®1£©…ŤĹĽĶ„ ĹŇ◊őÔŌŖĹ‚őŲ Ĺő™y=a£®x©Ā1£©£®x©Ā3£©£¨»Ľļůį—CĶ„◊ÝĪÍīķ»Ž«ů≥ŲaľīŅ…Ķ√ĶĹŇ◊őÔŌŖĹ‚őŲ Ĺ£Ľ£®2£©Ō»ņŻ”√īż∂®ŌĶ ż∑®«ů≥Ų÷ĪŌŖBEĶńĹ‚őŲ Ĺő™y= ![]() x©Ā1£¨÷ĪŌŖBCĶńĹ‚őŲ Ĺő™y=
x©Ā1£¨÷ĪŌŖBCĶńĹ‚őŲ Ĺő™y= ![]() x©Ā2£¨‘ŔĹ‚∑Ĺ≥Ő◊ť
x©Ā2£¨‘ŔĹ‚∑Ĺ≥Ő◊ť 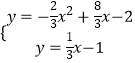 Ķ√F£®
Ķ√F£® ![]() £¨©Ā
£¨©Ā ![]() £©£ĽĹ”◊Ň»∑∂®H£®1£¨©Ā
£©£ĽĹ”◊Ň»∑∂®H£®1£¨©Ā ![]() £©£¨Ń¨Ĺ”AHĹĽBE”ŕQ£¨»ÁÕľ1£¨ņŻ”√Ķ„AļÕHĶńļŠ◊ÝĪÍŐō’ųĶ√ĶĹAH°Õx÷Š£¨ňý“‘Q£®1£¨©Ā
£©£¨Ń¨Ĺ”AHĹĽBE”ŕQ£¨»ÁÕľ1£¨ņŻ”√Ķ„AļÕHĶńļŠ◊ÝĪÍŐō’ųĶ√ĶĹAH°Õx÷Š£¨ňý“‘Q£®1£¨©Ā ![]() £©£¨»ĽļůņŻ”√»żĹ«–ő√śĽżĻę Ĺ£¨ņŻ”√S°ųFHB=S°ųBHQ+S°ųFHQĹÝ––ľ∆ň„£Ľ£®3£©Ō»«ů≥ŲD£®2£¨
£©£¨»ĽļůņŻ”√»żĹ«–ő√śĽżĻę Ĺ£¨ņŻ”√S°ųFHB=S°ųBHQ+S°ųFHQĹÝ––ľ∆ň„£Ľ£®3£©Ō»«ů≥ŲD£®2£¨ ![]() £©£¨÷ĪŌŖx=2ĹĽx÷Š”ŕN£¨»ÁÕľ2£¨÷§√ųRt°ųOMN°◊Rt°ųMBNĶ√ĶĹMN2=BNON£¨ľī£®t+
£©£¨÷ĪŌŖx=2ĹĽx÷Š”ŕN£¨»ÁÕľ2£¨÷§√ųRt°ųOMN°◊Rt°ųMBNĶ√ĶĹMN2=BNON£¨ľī£®t+ ![]() £©2=1°Ń2£¨»ĽļůĹ‚∑Ĺ≥ŐľīŅ…£Ľ£®4£©»ÁÕľ3£¨BPĹĽy÷Š”ŕG£¨ņŻ”√AB∆Ĺ∑÷°ŌFBPĶ√ĶĹĶ„G”ŽĶ„EĻō”ŕx÷Š∂‘≥∆£¨‘ÚG£®0£¨1£©£¨‘ŔņŻ”√īż∂®ŌĶ ż∑®«ů≥Ų÷ĪŌŖBQĶńĹ‚őŲ Ĺő™y=©Ā
£©2=1°Ń2£¨»ĽļůĹ‚∑Ĺ≥ŐľīŅ…£Ľ£®4£©»ÁÕľ3£¨BPĹĽy÷Š”ŕG£¨ņŻ”√AB∆Ĺ∑÷°ŌFBPĶ√ĶĹĶ„G”ŽĶ„EĻō”ŕx÷Š∂‘≥∆£¨‘ÚG£®0£¨1£©£¨‘ŔņŻ”√īż∂®ŌĶ ż∑®«ů≥Ų÷ĪŌŖBQĶńĹ‚őŲ Ĺő™y=©Ā ![]() x+1£¨»ĽļůĹ‚∑Ĺ≥Ő◊ť
x+1£¨»ĽļůĹ‚∑Ĺ≥Ő◊ť 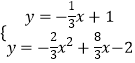 ľīŅ…Ķ√ĶĹPĶ„◊ÝĪÍ£ģ
ľīŅ…Ķ√ĶĹPĶ„◊ÝĪÍ£ģ


 ≥…Ļ¶—ĶŃ∑ľ∆ĽģŌĶŃ–īūįł
≥…Ļ¶—ĶŃ∑ľ∆ĽģŌĶŃ–īūįł Ī∂ňŔ—ĶŃ∑∑®÷ĪÕ®÷–ŅľŅľĶ„ŌĶŃ–īūįł
Ī∂ňŔ—ĶŃ∑∑®÷ĪÕ®÷–ŅľŅľĶ„ŌĶŃ–īūįł “ĽĺŪł„∂®ŌĶŃ–īūįł
“ĽĺŪł„∂®ŌĶŃ–īūįł √Ż–£◊ų“ĶĪĺŌĶŃ–īūįł
√Ż–£◊ų“ĶĪĺŌĶŃ–īūįł «Š«…∂ŠĻŕ÷‹≤‚‘¬Ņľ÷ĪÕ®√Ż–£ŌĶŃ–īūįł
«Š«…∂ŠĻŕ÷‹≤‚‘¬Ņľ÷ĪÕ®√Ż–£ŌĶŃ–īūįł
| ńÍľ∂ | łŖ÷–Ņő≥Ő | ńÍľ∂ | ≥ű÷–Ņő≥Ő |
| łŖ“Ľ | łŖ“Ľ√‚∑—Ņő≥ŐÕ∆ľŲ£° | ≥ű“Ľ | ≥ű“Ľ√‚∑—Ņő≥ŐÕ∆ľŲ£° |
| łŖ∂Ģ | łŖ∂Ģ√‚∑—Ņő≥ŐÕ∆ľŲ£° | ≥ű∂Ģ | ≥ű∂Ģ√‚∑—Ņő≥ŐÕ∆ľŲ£° |
| łŖ»ż | łŖ»ż√‚∑—Ņő≥ŐÕ∆ľŲ£° | ≥ű»ż | ≥ű»ż√‚∑—Ņő≥ŐÕ∆ľŲ£° |
Ņ∆ńŅ£ļ≥ű÷– ż—ß ņī‘ī£ļ Ő‚–Õ£ļ
°ĺŐ‚ńŅ°Ņ‘ń∂ŃņŪĹ‚£ļ»ÁÕľ1£¨‘ŕ∆Ĺ√śńŕ—°“Ľ∂®Ķ„O£¨“ż“ĽŐű”–∑ĹŌÚĶń…šŌŖOx£¨‘Ŕ—°∂®“ĽłŲĶ•őĽ≥§∂»£¨ń«√ī∆Ĺ√ś…Ō»ő“ĽĶ„MĶńőĽ÷√Ņ…”…°ŌMOxĶń∂» ż¶»”ŽOMĶń≥§∂»m»∑∂®£¨”––Ú ż∂‘£®¶»£¨m£©≥∆ő™MĶ„Ķń°įľę◊ÝĪÍ°Ī£¨’‚—ýĹ®ŃĘĶń◊ÝĪÍŌĶ≥∆ő™°įľę◊ÝĪÍŌĶ°Ī£ģ ”¶”√£ļ‘ŕÕľ2Ķńľę◊ÝĪÍŌĶŌ¬£¨»ÁĻŻ’żŃýĪŖ–őĶńĪŖ≥§ő™2£¨”–“ĽĪŖOA‘ŕ…šŌŖOx…Ō£¨‘Ú’żŃýĪŖ–őĶń∂•Ķ„CĶńľę◊ÝĪÍ”¶ľ«ő™£® £©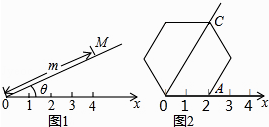
A.£®60°„£¨4£©
B.£®45°„£¨4£©
C.£®60°„£¨2 ![]() £©
£©
D.£®50°„£¨2 ![]() £©
£©
≤ťŅīīūįłļÕĹ‚őŲ>>
Ņ∆ńŅ£ļ≥ű÷– ż—ß ņī‘ī£ļ Ő‚–Õ£ļ
°ĺŐ‚ńŅ°Ņ»ÁÕľ£¨6łŲ–ő◊ī°Ęīů–°ÕÍ»ęŌŗÕ¨ĶńŃ‚–ő◊ť≥…ÕÝłŮ£¨“—÷™Ń‚–őĶń“ĽłŲĹ«°ŌOő™60°„£¨A£¨B£¨C∂ľ‘ŕłŮĶ„…Ō£¨‘Útan°ŌABCĶń÷Ķő™ £ģ 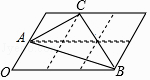
≤ťŅīīūįłļÕĹ‚őŲ>>
Ņ∆ńŅ£ļ≥ű÷– ż—ß ņī‘ī£ļ Ő‚–Õ£ļ
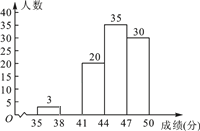
°ĺŐ‚ńŅ°Ņő™Ńňīę≥–”Ň–„īęÕ≥őńĽĮ£¨ő“ –◊ť÷ĮŃň“Ľīő≥ű»żńÍľ∂1 200√Ż—ß…ķ≤őľ”Ķń°įļļ◊÷Őż–ī°Īīů»Ł£¨ő™ŃňłŁļ√ĶōŃňĹ‚Īĺīőīů»ŁĶń≥…ľ®∑÷≤ľ«ťŅŲ£¨ňśĽķ≥ť»°Ńň100√Ż—ß…ķĶń≥…ľ®(¬ķ∑÷50∑÷)£¨’ŻņŪĶ√ĶĹ»ÁŌ¬ĶńÕ≥ľ∆ÕľĪŪ£ļ
≥…ľ®(∑÷) | 36 | 37 | 38 | 39 | 40 | 41 | 42 | 43 | 44 | 45 | 46 | 47 | 48 | 49 | 50 |
»ň ż | 1 | 2 | 3 | 3 | 6 | 7 | 5 | 8 | 15 | 9 | 11 | 12 | 8 | 6 | 4 |
≥…ľ®∑÷◊ť | ∆Ķ ż | ∆Ķ¬ (įŔ∑÷Ī») |
35°‹x<38 | 3 | 0.03 |
38°‹x<41 | a | 0.12 |
41°‹x<44 | 20 | 0.20 |
44°‹x<47 | 35 | 0.35 |
47°‹x°‹50 | 30 | b |
«Žłýĺ›ňýŐŠĻ©Ķń–ŇŌĘĹ‚īūŌ¬Ń–ő Ő‚£ļ
(1)∆Ķ¬ Õ≥ľ∆ĪŪ÷–a£Ĺ________£¨b£Ĺ_______£Ľ
(2)«Ž≤Ļ»ę∆Ķ ż∑÷≤ľ÷Ī∑ĹÕľ£Ľ
(3)«Žłýĺ›≥ť—ýÕ≥ľ∆ĹŠĻŻ£¨Ļņľ∆ł√īőīů»Ł÷–≥…ľ®≤ĽĶÕ”ŕ41∑÷Ķń—ß…ķ”–∂ŗ…Ŕ»ň£Ņ
≤ťŅīīūįłļÕĹ‚őŲ>>
Ņ∆ńŅ£ļ≥ű÷– ż—ß ņī‘ī£ļ Ő‚–Õ£ļ
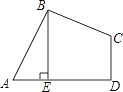
°ĺŐ‚ńŅ°Ņ»ÁÕľ£¨‘ŕňńĪŖ–őABCD÷–£¨AB=BC£¨°ŌABC=°ŌCDA=90°„£¨BE°ÕAD”ŕĶ„E£¨«“ňńĪŖ–őABCDĶń√śĽżő™4£¨‘ÚBEĶ»”ŕ________£ģ
≤ťŅīīūįłļÕĹ‚őŲ>>
Ņ∆ńŅ£ļ≥ű÷– ż—ß ņī‘ī£ļ Ő‚–Õ£ļ
°ĺŐ‚ńŅ°Ņń≥¬÷ī¨Õý∑Ķ”ŕA°ĘBŃĹĶō÷ģľš£¨…Ťī¨‘ŕĺ≤ňģ÷–ĶńňŔ∂»≤ĽĪš£¨ń«√ī£¨ĶĪňģĶńŃųňŔ‘Ųīů Ī£¨¬÷ī¨Õý∑Ķ“Ľīőňý”√Ķń Īľš£®°°°°£©
A. ≤ĽĪš B. ‘Ųľ” C. ľű…Ŕ D. ‘Ųľ”£¨ľű…Ŕ∂ľ”–Ņ…ń‹
≤ťŅīīūįłļÕĹ‚őŲ>>
Ņ∆ńŅ£ļ≥ű÷– ż—ß ņī‘ī£ļ Ő‚–Õ£ļ
°ĺŐ‚ńŅ°Ņń≥įŗő™¬ķ◊„Õ¨—ß√«ŅőÕ‚ĽÓ∂ĮĶń–Ť«ů£¨“™«ůĻļŇŇ«ÚļÕ◊„«Ú»Űł…łŲ.“—÷™◊„«ÚĶńĶ•ľŘĪ»ŇŇ«ÚĶńĶ•ľŘ∂ŗ![]() ‘™£¨”√
‘™£¨”√![]() ‘™ĻļĶ√ĶńŇŇ«Ú żŃŅ”Ž”√
‘™ĻļĶ√ĶńŇŇ«Ú żŃŅ”Ž”√![]() ‘™ĻļĶ√Ķń◊„«Ú żŃŅŌŗĶ».
‘™ĻļĶ√Ķń◊„«Ú żŃŅŌŗĶ».
ĘŇŇŇ«ÚļÕ◊„«ÚĶńĶ•ľŘłų «∂ŗ…Ŕ‘™£Ņ
Ę∆»Ű«°ļ√”√»•![]() ‘™£¨”–ńńľł÷÷Ļļ¬Ú∑Ĺįł£Ņ
‘™£¨”–ńńľł÷÷Ļļ¬Ú∑Ĺįł£Ņ
≤ťŅīīūįłļÕĹ‚őŲ>>
Ņ∆ńŅ£ļ≥ű÷– ż—ß ņī‘ī£ļ Ő‚–Õ£ļ
°ĺŐ‚ńŅ°ŅĻō”ŕxĶń∑Ĺ≥Őx2+£®2k+1£©x+k2+2=0”–ŃĹłŲ Ķ żłýx1°Ęx2
£®1£©«ů Ķ żkĶń»°÷Ķ∑∂őߣĽ
£®2£©»Űx1°Ęx2¬ķ◊„|x1|+|x2|=|x1x2|©Ā1£¨«ůkĶń÷Ķ£ģ
≤ťŅīīūįłļÕĹ‚őŲ>>
Ņ∆ńŅ£ļ≥ű÷– ż—ß ņī‘ī£ļ Ő‚–Õ£ļ
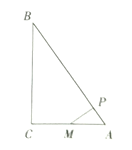
°ĺŐ‚ńŅ°Ņ»ÁÕľ£¨‘ŕ°ųABC÷–£¨°ŌC=90°„£¨AM=CM£¨MP°ÕAB”ŕĶ„P.«ů÷§£ļBP2=AP2+BC2.
≤ťŅīīūįłļÕĹ‚őŲ>>
įŔ∂»÷¬–Ň - Ń∑Ōį≤ŠŃ–ĪŪ - ‘Ő‚Ń–ĪŪ
ļĢĪĪ °Ľ•Ń™ÕÝő•∑®ļÕ≤ĽŃľ–ŇŌĘĺŔĪ®∆ĹŐ® | ÕÝ…Ō”–ļ¶–ŇŌĘĺŔĪ®◊®«Ý | ĶÁ–Ň’©∆≠ĺŔĪ®◊®«Ý | …śņķ ∑–ťőř÷ų“Ś”–ļ¶–ŇŌĘĺŔĪ®◊®«Ý | …ś∆ů«÷»®ĺŔĪ®◊®«Ý
ő•∑®ļÕ≤ĽŃľ–ŇŌĘĺŔĪ®ĶÁĽį£ļ027-86699610 ĺŔĪ®” Ōš£ļ58377363@163.com