【题目】为节约用水，某区规定三口之家每月标准用水量为15立方米，不超过标准的水费价格为每立方米1.5元，超过标准的超过部分的价格为每立方米3元，小明家11月份用水x立方米；小红家11月份用水y（y＞15）立方米
（1）用含y的代数式表示小红家11月份应缴的水费；
（2）用含有x的代数式表示小明家11月份应缴的水费.
【答案】（1）小红家11月份应缴的水费为
；（2）当x小于或等于15时，小明家11月份应缴的水费为1.5x； 当x＞15时，小明家11月份应缴的水费为
【解析】
（1）水费分两部分：15立方米按1.5元∕立方米收费，超过部分（y-15）按3元∕立方米收费，然后把两者相加即可；
（2）分两种情况讨论，①不超过部分水费为1.5元∕立方米，用x乘以1.5即可；
②水费分两部分：15立方米按1.5元∕立方米收费，超过部分（x-15）按3元∕立方米收费，然后把两者相加即可；
（1）∵y＞15∴小红家11月份应缴的水费：
；
（2）当x小于或等于15时，小明家11月份应缴的水费：1.5x；
当x＞15时，小明家11月份应缴的水费：
.
阅读快车系列答案科目：初中数学 来源： 题型：
【题目】根据下列语句，画出图形并回答问题．
如图，已知三点A，B，C．
（1）分别作直线AB和射线AC；
（2）作线段BC, 取BC的中点D；
（3）连接AD；
（4）用量角器度量出∠ADB的度数最接近（ ）
A.80° B. 90° C. 100° D. 110°
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】菱形ABCD中,两条对角线AC、BD相交于点O,点E和点F分别是BC和CD上一动点,且∠EOF+∠BCD=180°，连接EF.
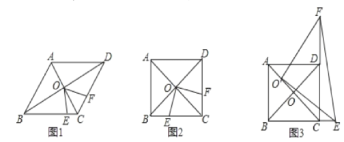
(1)如图2,当∠ABC=60°时，猜想三条线段CE、CF、AB之间的数量关系___；
(2)如图1,当∠ABC=90°时,若AC=4
,BE=
，求线段EF的长；
(3)如图3,当∠ABC=90°,将∠EOF的顶点移到AO上任意一点O′处,∠EO′F绕点O′旋转,仍满足∠EO′F+∠BCD=180°,O′E交BC的延长线一点E,射线O′F交CD的延长线上一点F,连接EF探究在整个运动变化过程中,线段CE、CF,O′C之间满足的数量关系，请直接写出你的结论.
查看答案和解析>>
科目：初中数学 来源： 题型：
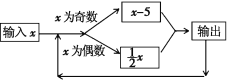
【题目】按如图所示的程序计算，如果开始输入的x的值为48，我们发现第一次输出得到的结果为24，第二次输出的结果为12，第三次得到的输出结果为6，……，则第2019次得到的结果为__.
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】水稻种植是嘉兴的传统农业.为了比较甲、乙两种水稻秧苗的长势,农技人员从两块试验田中分别随机抽取5株水稻秧苗,将测得的苗高数据绘制成如图所示的统计图.
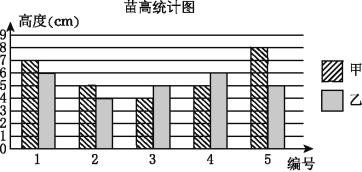
请你根据统计图所提供的数据,计算甲、乙两种水稻苗高的平均数和方差,并比较两种水稻的长势.
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】同学们都知道，
表示4与-2的差的绝对值，实际上也可理解为4与-2两数在数轴上所对应的两点之间的距离，同理
也可理解为
与3两数在数轴上所对应的两点之间的距离，
就表示在数轴上对应的点到-1的距离，由上面绝对值的几何意义，解答下列问题：
（1）求
.
（2）若
，则
.
（3）请你找出所有符合条件的整数，使得
.
（4）求
的最小值，并写出此时的取值情况.
（5）已知
，求
的最大值和最小值.
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】已知抛物线
（m是常数）的顶点为P，直线l：y=x﹣1
（1）求证：点P在直线l上；
（2）当m=﹣3时，抛物线与x轴交于A，B两点，与y轴交于点C，与直线l的另一个交点为Q，M是x轴下方抛物线上的一点，∠ACM=∠PAQ（如图），求点M的坐标；
（3）若以抛物线和直线l的两个交点及坐标原点为顶点的三角形是等腰三角形，请直接写出所有符合条件的m的值．
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com
