
【题目】蜗牛从某点![]() 开始沿东西方向的直线爬行,规定向东爬行的路程记为正数,向西爬行的路程记为负数.爬过的各段路程依次为(单位:厘米):
开始沿东西方向的直线爬行,规定向东爬行的路程记为正数,向西爬行的路程记为负数.爬过的各段路程依次为(单位:厘米):![]()
(1)蜗牛最后是否回到出发点?请说明理由;
(2)蜗牛离开出发点![]() 最远时是_______厘米;
最远时是_______厘米;
(3)在爬行过程中,如果蜗牛每爬2厘米奖励一粒芝麻,求蜗牛-共得到多少粒芝麻?
【答案】(1)能,见解析;(2)14;(3)124
【解析】
(1)将各次的路程相加即可得到答案;
(2)分别计算每次离开的距离进行比较即可得到结果;
(3)将所有的爬行距离相加再乘以2即可得到答案.
(1)回到了原点,
∵6-4+12-8-4+13-15=0(厘米),
∴蜗牛最后回到了原点;
(2)第一次离开的距离是6厘米,
第二次离开的距离是6-4=2厘米,
第三次离开的距离是2+12=14厘米,
第四次离开的距离是14-8=4厘米,
第五次离开的距离是4-4=0厘米,
第六次离开的距离是0+13=13厘米,
第七次离开的距离是![]() 厘米,
厘米,
∴蜗牛离开出发点![]() 最远时是14厘米,
最远时是14厘米,
故答案为:14;
(3)![]() =124(粒)
=124(粒)
∴蜗牛-共得到124粒芝麻.


科目:初中数学 来源: 题型:
【题目】如图所示,点D在![]() 的AB边上,且
的AB边上,且![]() .
.
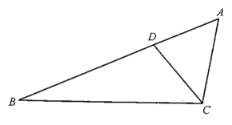
(1)作![]() 的平分线DE,交BC于点E(用尺规作图法,保留作图痕迹,不要求写作法);
的平分线DE,交BC于点E(用尺规作图法,保留作图痕迹,不要求写作法);
(2)在(1)的条件下,判断直线DE与直线AC的位置关系.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图1,两块直角三角纸板(Rt△ABC和Rt△BDE)按图所示的方式摆放(重合点为B),其中∠BDE=∠ACB=90°,∠ABC=30°,BD=DE=AC=2.将△BDE绕着点B顺时针旋转.
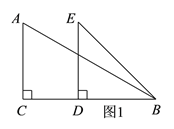
(1)当点D在BC上时,求CD的长;
(2)当△BDE旋转到A,D,E三点共线时,求△CDE的面积;
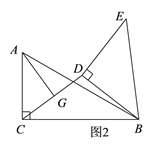
(3)如图2,连接CD,点G是CD的中点,连接AG,求AG的最大值和最小值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某工厂计划生产480个零件.当生产任务完成一半时,停止生产进行反思和改进,用时20分钟.恢复生产后工作效率比原来可以提高20%,要求比原计划提前40分钟完成任务,那么反思改进后每小时需要生产多少个零件?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图(1),在Rt△ABC,∠ACB=90°,分别以AB、BC为一边向外作正方形ABFG、BCED,连结AD、CF,AD与CF交于点M;
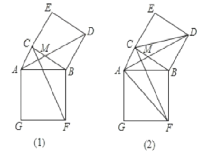
(1)求证:△ABD≌△FBC;
(2) 如图(2),已知AD=6,求四边形AFDC的面积;
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知:如图1,在平面直角坐标系中,点O为坐标原点,点A在x轴正半轴上,点C在第一象限,且∠COA=60°,以OA、OC为邻边作菱形OABC,且菱形OABC的面积为![]() .
.
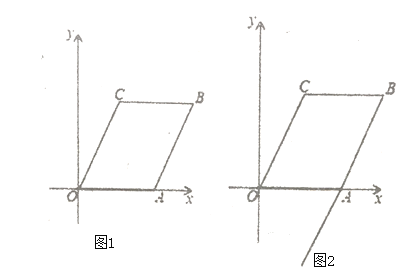
(1)求B. C两点的坐标;
(2)动点P从C点出发沿射线CB匀速运动,同时动点Q从A点出发沿射线BA的方向匀速运动,P、Q两点的运动速度均为2个单位/秒,连接PQ和AC,PQ和AC所在直线交于点D,点E为线段BQ的中点,连接DE,设动点P、Q的运动时间为t,请将△DQE的面积S用含t的式子表示,并直接写出t的取值范围;
(3)在(2)的条件下,过点Q作QF⊥y轴于点F,当t为何值时,以P、B.、F.、Q为顶点的四边形为平行四边形?
查看答案和解析>>
科目:初中数学 来源: 题型:
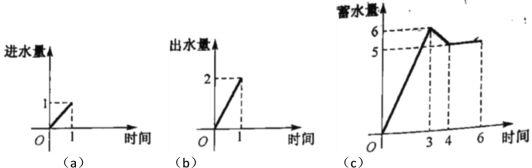
【题目】一水池有两个进水口,一个出水口,一个水口在单位时间内的进、出水量如图(a)、(b)所示,某天从0点到6点,该水池的蓄水量如图(c)所示,给出以下3个论断:①0点到3点只进水不出水;②3点到4点不进水只出水;③4点到6点一定不进水不出水.则正确的论断是________.(填上所有正确论断的序号)
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com