
”¾ĢāÄæ”æij³ĒŹŠ¾ÓĆńÓĆĖ®ŹµŠŠ½×ĢŻŹÕ·Ń£¬Ć滧ĆæŌĀÓĆĖ®ĮæČē¹ūĪ“³¬¹ż20¶Ö£¬°“Ćæ¶Ö![]() ŌŖŹÕ·Ń
ŌŖŹÕ·Ń![]() Čē¹ū³¬¹ż20¶Ö£¬Ī“³¬¹żµÄ²æ·Ö°“Ćæ¶Ö
Čē¹ū³¬¹ż20¶Ö£¬Ī“³¬¹żµÄ²æ·Ö°“Ćæ¶Ö![]() ŌŖŹÕ·Ń£¬³¬¹żµÄ²æ·Ö°“Ćæ¶Ö
ŌŖŹÕ·Ń£¬³¬¹żµÄ²æ·Ö°“Ćæ¶Ö![]() ŌŖŹÕ·Ń
ŌŖŹÕ·Ń![]() Éčij»§ĆæŌĀÓĆĖ®ĮæĪŖx¶Ö£¬Ó¦ŹÕĖ®·ŃĪŖyŌŖ£®
Éčij»§ĆæŌĀÓĆĖ®ĮæĪŖx¶Ö£¬Ó¦ŹÕĖ®·ŃĪŖyŌŖ£®
![]() Éčij»§¾ÓĆńĆæŌĀÓĆĖ®ĮæĪŖm¶Ö
Éčij»§¾ÓĆńĆæŌĀÓĆĖ®ĮæĪŖm¶Ö![]() £¬ŌņÓ¦ŹÕĖ®·ŃĪŖ______ŌŖ
£¬ŌņÓ¦ŹÕĖ®·ŃĪŖ______ŌŖ![]() ÓĆŗ¬mµÄ“śŹżŹ½±ķŹ¾
ÓĆŗ¬mµÄ“śŹżŹ½±ķŹ¾![]() £»
£»
![]() Éčij»§¾ÓĆńĆæŌĀÓĆĖ®ĮæĪŖm¶Ö
Éčij»§¾ÓĆńĆæŌĀÓĆĖ®ĮæĪŖm¶Ö![]() £¬ŌņÓ¦ŹÕĖ®·ŃĪŖ______ŌŖ
£¬ŌņÓ¦ŹÕĖ®·ŃĪŖ______ŌŖ![]() ÓĆŗ¬mµÄ“śŹżŹ½±ķŹ¾
ÓĆŗ¬mµÄ“śŹżŹ½±ķŹ¾![]() £»
£»
![]() ČōøĆ³ĒŹŠÄ³»§5ŌĀ·ŻĖ®·ŃĘ½¾łĪŖĆæ¶Ö
ČōøĆ³ĒŹŠÄ³»§5ŌĀ·ŻĖ®·ŃĘ½¾łĪŖĆæ¶Ö![]() ŌŖ£¬ĒóøĆ»§5ŌĀ·ŻÓĆĖ®¶ąÉŁ¶Ö£æ
ŌŖ£¬ĒóøĆ»§5ŌĀ·ŻÓĆĖ®¶ąÉŁ¶Ö£æ
”¾“š°ø”æ£Ø1£©1.9m””£Ø2£©2.8m©18””£Ø3£©30
”¾½āĪö”æ
ŹŌĢā£Ø1£©ŅņĪŖŌĀÓĆĖ®Įæ²»³¬¹ż20¶ÖŹ±£¬°“1.9ŌŖ/¶Ö¼Ę·Ń£¬ĖłŅŌµ±m”Ü20Ź±£¬Ó¦ŹÕĖ°·Ń1.9m£»
£Ø2£©ŅņĪŖŌĀÓĆĖ®Į泬¹ż20¶ÖŹ±£¬ĘäÖŠµÄ20¶ÖČŌ°“1.9ŌŖ/¶ÖŹÕ·Ń£¬³¬¹ż²æ·Ö°“2.8ŌŖ/¶Ö¼Ę·Ń£¬ĖłŅŌµ±x£¾20Ź±£¬Ó¦ŹÕĖ®·ŃĪŖ 1.9”Į20+2.8£Øm-20£©=2.8m-18£»
£Ø3£©ÓÉĢāŅāæÉµĆ£ŗ5ŌĀ·ŻÓĆĖ®µÄĮ泬¹żĮĖ20¶Ö£¬Č»ŗóæÉøł¾ŻĘ½¾łĆæ¶ÖµÄÓĆĖ®ĮææɵĆ2.8m-18=2.2m£¬Ēó½ā¼“æÉ£®
ŹŌĢā½āĪö£ŗ£Ø1£©1.9m””
£Ø2£©2.8m©18””
£Ø3£©”ß5ŌĀ·ŻĖ®·ŃĘ½¾łĪŖĆæ¶Ö2.2ŌŖ£¬ÓĆĖ®ĮæČē¹ūĪ“³¬¹ż20¶Ö£¬°“Ćæ¶Ö1.9ŌŖŹÕ·Ń£®
”ąÓĆĖ®Į泬¹żĮĖ20¶Ö£®
2.8x©18=2.2x£¬
x=30£®
“š£ŗøĆ»§5ŌĀ·ŻÓĆĖ®30¶Ö£®


 ѧĮ·æģ³µµĄæģĄÖ¼ŁĘŚŗ®¼Ł×÷ŅµĻµĮŠ“š°ø
ѧĮ·æģ³µµĄæģĄÖ¼ŁĘŚŗ®¼Ł×÷ŅµĻµĮŠ“š°ø ŠĀĖ¼Ī¬ŗ®¼Ł×÷ŅµĻµĮŠ“š°ø
ŠĀĖ¼Ī¬ŗ®¼Ł×÷ŅµĻµĮŠ“š°ø
| Äź¼¶ | øßÖŠæĪ³Ģ | Äź¼¶ | ³õÖŠæĪ³Ģ |
| øßŅ» | øßŅ»Ćā·ŃæĪ³ĢĶĘ¼ö£” | ³õŅ» | ³õŅ»Ćā·ŃæĪ³ĢĶĘ¼ö£” |
| ø߶ž | ø߶žĆā·ŃæĪ³ĢĶĘ¼ö£” | ³õ¶ž | ³õ¶žĆā·ŃæĪ³ĢĶĘ¼ö£” |
| øßČż | øßČżĆā·ŃæĪ³ĢĶĘ¼ö£” | ³õČż | ³õČżĆā·ŃæĪ³ĢĶĘ¼ö£” |
æĘÄæ£ŗ³õÖŠŹżŃ§ Ą“Ō“£ŗ ĢāŠĶ£ŗ
”¾ĢāÄæ”æČēĶ¼£¬Ö±Ļßy1=kx+bÓėĖ«ĒśĻßy2= ![]() ½»ÓŚA”¢BĮ½µć£¬ĖüĆĒµÄŗį×ų±ź·Ö±šĪŖ1ŗĶ5£®
½»ÓŚA”¢BĮ½µć£¬ĖüĆĒµÄŗį×ų±ź·Ö±šĪŖ1ŗĶ5£® 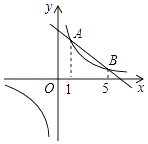
£Ø1£©µ±m=5Ź±£¬ĒóÖ±ĻßABµÄ½āĪöŹ½¼°”÷AOBµÄĆ껿£»
£Ø2£©µ±y1£¾y2Ź±£¬Ö±½ÓŠ“³öxµÄȔֵ·¶Ī§£®
²éæ““š°øŗĶ½āĪö>>
æĘÄæ£ŗ³õÖŠŹżŃ§ Ą“Ō“£ŗ ĢāŠĶ£ŗ
”¾ĢāÄæ”æČēĶ¼£¬ŌŚ”÷ABCÖŠ£¬”ĻBAC=50”ć£¬°Ń”÷ABCŃŲEFÕŪµž£¬C¶ŌÓ¦µćĒ”ŗĆÓė”÷ABCµÄĶāŠÄOÖŲŗĻ£¬Ōņ”ĻCFEµÄ¶ČŹżŹĒ£Ø £© 
A.40”ć
B.45”ć
C.50”ć
D.55”ć
²éæ““š°øŗĶ½āĪö>>
æĘÄæ£ŗ³õÖŠŹżŃ§ Ą“Ō“£ŗ ĢāŠĶ£ŗ
”¾ĢāÄæ”æŅŃÖŖa”¢b·Ö±š¶ŌÓ¦ŹżÖįÉĻA”¢BĮ½µć£¬²¢ĒŅĀś×ć|a©2|+£Ø3a+2b£©2=0£¬µćPĪŖŹżÖįÉĻŅ»øö¶Æµć£¬Ėü¶ŌÓ¦µÄŹżŹĒx
£Ø1£©ĢīæÕ£ŗa=”” ””£¬b=”” ””£¬AB=”” ””£»
£Ø2£©ČōPĪŖĻ߶ĪABÉĻŅ»µć£¬²¢ĒŅPA=3PB£¬ĒóxµÄÖµ£»
£Ø3£©ČōPµć“ÓAµć³ö·¢ŅŌĆæĆė2øöµ„Ī»µÄĖŁ¶ČŌĖ¶Æ£¬ÄĒĆ“³ö·¢¼øĆėÖÓŗó£¬Ļ߶ĪPA=4PB£æ
![]()
²éæ““š°øŗĶ½āĪö>>
æĘÄæ£ŗ³õÖŠŹżŃ§ Ą“Ō“£ŗ ĢāŠĶ£ŗ
”¾ĢāÄæ”æÓĆ”°”ī”±¶ØŅåŅ»ÖÖŠĀŌĖĖć£ŗ¶ŌÓŚČĪŅāÓŠĄķŹżaŗĶb£¬¹ę¶Øa”īb=ab2+2ab+a£®
Čē£ŗ1”ī3=1”Į32+2”Į1”Į3+1=16£®
£Ø1£©Ēó£Ø©2£©”ī3µÄÖµ£»
£Ø2£©Čō£Ø![]() ”ī3£©”ī£Ø©
”ī3£©”ī£Ø©![]() £©=8£¬ĒóaµÄÖµ£»
£©=8£¬ĒóaµÄÖµ£»
£Ø3£©Čō2”īx=m£¬£Ø![]() x£©”ī3=n£ØĘäÖŠxĪŖÓŠĄķŹż£©£¬ŹŌ±Č½Ļm£¬nµÄ“󊔣®
x£©”ī3=n£ØĘäÖŠxĪŖÓŠĄķŹż£©£¬ŹŌ±Č½Ļm£¬nµÄ“󊔣®
²éæ““š°øŗĶ½āĪö>>
æĘÄæ£ŗ³õÖŠŹżŃ§ Ą“Ō“£ŗ ĢāŠĶ£ŗ
”¾ĢāÄæ”æČēĶ¼ĖłŹ¾µÄĶ¼ŠĪÖŠ£¬ĖłÓŠµÄĖıߊĪ¶¼ŹĒÕż·½ŠĪ£¬ĖłÓŠµÄČż½ĒŠĪ¶¼ŹĒÖ±½ĒČż½ĒŠĪ£¬ĘäÖŠ×ī“óµÄÕż·½ŠĪµÄ±ß³¤ĪŖ7cm£¬ŌņĖłÓŠÕż·½ŠĪµÄĆ껿µÄŗĶŹĒ£Ø £©cm2
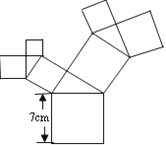
A. 28 B. 49 C. 98 D. 147
²éæ““š°øŗĶ½āĪö>>
æĘÄæ£ŗ³õÖŠŹżŃ§ Ą“Ō“£ŗ ĢāŠĶ£ŗ
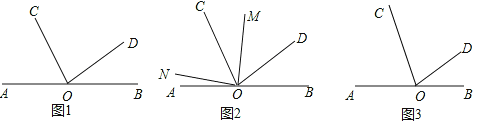
”¾ĢāÄæ”æŅŃÖŖ£¬µćOŹĒÖ±ĻßABÉĻŅ»µć£¬OC”¢ODĪŖ“ÓµćOŅż³öµÄĮ½ĢõÉäĻߣ¬”ĻBOD=30”ć£¬”ĻCOD=![]() ”ĻAOC£®
”ĻAOC£®
£Ø1£©ČēĶ¼¢Ł£¬Ēó”ĻAOCµÄ¶ČŹż£»
£Ø2£©ČēĶ¼¢Ś£¬ŌŚ”ĻAODµÄÄŚ²æ×÷”ĻMON=90”ć£¬ĒėÖ±½ÓŠ“³ö”ĻAONÓė”ĻCOMÖ®¼äµÄŹżĮæ¹ŲĻµ”” ””£»
£Ø3£©ŌŚ£Ø2£©µÄĢõ¼žĻĀ£¬ČōOMĪŖ”ĻBOCµÄ½ĒĘ½·ÖĻߣ¬ŹŌĖµĆ÷”ĻAON=”ĻCON£®
²éæ““š°øŗĶ½āĪö>>
æĘÄæ£ŗ³õÖŠŹżŃ§ Ą“Ō“£ŗ ĢāŠĶ£ŗ
”¾ĢāÄæ”æČēĶ¼£¬·Ö±šŅŌĻ߶ĪACµÄĮ½øö¶ĖµćA£¬CĪŖŌ²ŠÄ£¬“óÓŚ![]() ACµÄ³¤ĪŖ°ė¾¶»»”£¬Į½»”Ļą½»ÓŚB£¬DĮ½µć£¬Į¬½ÓBD£¬AB£¬BC£¬CD£¬DA£¬ŅŌĻĀ½įĀŪ£ŗ
ACµÄ³¤ĪŖ°ė¾¶»»”£¬Į½»”Ļą½»ÓŚB£¬DĮ½µć£¬Į¬½ÓBD£¬AB£¬BC£¬CD£¬DA£¬ŅŌĻĀ½įĀŪ£ŗ
¢ŁBD“¹Ö±Ę½·ÖAC£»
¢ŚACĘ½·Ö”ĻBAD£»
¢ŪAC=BD£»
¢ÜĖıߊĪABCDŹĒÖŠŠÄ¶Ō³ĘĶ¼ŠĪ£®
ĘäÖŠÕżČ·µÄÓŠ£Ø £©
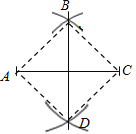
A. ¢Ł¢Ś¢Ū B. ¢Ł¢Ū¢Ü C. ¢Ł¢Ś¢Ü D. ¢Ś¢Ū¢Ü
²éæ““š°øŗĶ½āĪö>>
æĘÄæ£ŗ³õÖŠŹżŃ§ Ą“Ō“£ŗ ĢāŠĶ£ŗ
”¾ĢāÄæ”æŌŚ¾ŲŠĪABCDÖŠ£¬”ĻABCµÄĘ½·ÖĻß½»ADÓŚµćE£¬”ĻBEDµÄĘ½·ÖĻß½»DCÓŚµćF£¬ČōAB=6£¬µćFĒ”ĪŖDCµÄÖŠµć£¬ŌņBC=£Ø½į¹ū±£ĮōøłŗÅ£©
²éæ““š°øŗĶ½āĪö>>
°Ł¶ČÖĀŠÅ - Į·Ļ°²įĮŠ±ķ - ŹŌĢāĮŠ±ķ
ŗž±±Ź”»„ĮŖĶųĪ„·ØŗĶ²»Į¼ŠÅĻ¢¾Ł±ØĘ½ĢØ | ĶųÉĻÓŠŗ¦ŠÅĻ¢¾Ł±Ø×ØĒų | µēŠÅÕ©Ę¾Ł±Ø×ØĒų | É꥜Ź·ŠéĪŽÖ÷ŅåÓŠŗ¦ŠÅĻ¢¾Ł±Ø×ØĒų | ÉęĘóĒÖČؾŁ±Ø×ØĒų
Ī„·ØŗĶ²»Į¼ŠÅĻ¢¾Ł±Øµē»°£ŗ027-86699610 ¾Ł±ØÓŹĻä£ŗ58377363@163.com