设P＝.Q＝.R＝．则P.Q.R的大小关系为 [ ] A．P＞Q＞RB．Q＞P＞R C．P＞R＞QD．R＞Q＞P 题目和参考答案——青夏教育精英家教网—

精英家教网 > 初中数学 > 题目详情

设P＝，Q＝，R＝．则P、Q、R的大小关系为

[　　]

A．P＞Q＞R

B．Q＞P＞R

C．P＞R＞Q

D．R＞Q＞P

答案：A

练习册系列答案

68所名校图书小升初高分夺冠真卷系列答案

伴你成长周周练月月测系列答案

小升初金卷导练系列答案

萌齐小升初强化模拟训练系列答案

年级	高中课程	年级	初中课程
高一	高一免费课程推荐！	初一	初一免费课程推荐！
高二	高二免费课程推荐！	初二	初二免费课程推荐！
高三	高三免费课程推荐！	初三	初三免费课程推荐！
更多初中、高中辅导课程推荐,点击进入>>

相关习题

科目：初中数学 来源： 题型：044

传说波斯国王，出了下列算题悬赏大臣：

我的3只金碗里放着数目相同的珍珠，我把第一只金碗里的珍珠的一半给我大儿子，把第二只金碗里的珍珠的给我二儿子，把第三只金碗里的珍珠的给我的小儿子，然后再把第一只金碗里的4颗珍珠给我大女儿，把第二只金碗里的6颗珍珠给我二女儿，把第三只金碗里的2颗珍珠给我小女儿，这样第一只金碗里剩下38颗珍珠，第二只金碗里剩下22颗珍珠，第三只金碗里剩下19颗珍珠，试问：我的3只金碗里原来分别放着多少颗珍珠?

第一个大臣认为第一只金碗里的一半为(38＋4)颗，所以第一只金碗里有2(38＋4)＝84(颗)．第二只金碗里的为(22+6)颗，所以第二只金碗里有3(22+6)＝84(颗)．第三只金碗里的为(19＋2)颗，所以第三只金碗里有4(19+2)＝84(颗)．所以国王三只金碗里分别放着84颗珍珠．

第二个大臣设第一只金碗里有x颗珍珠，由题意列出方程x＋4＋38＝x解得x＝84，设第二只金碗里有y颗珍珠，由题意列出方程专y＋6＋22＝y，解得y＝84，设第三只金碗里有z颗珍珠，由题意列出方程z＋2＋19＝z，解得z＝84．所以国王三只金碗里分别放着84颗珍珠

第三个大臣设国王的每只金碗里放着x颗珍珠，a代表国王给儿子的珍珠占碗里的珍珠数的几分之几，b代表国王给女儿的珍珠数，c代表碗里剩下的珍珠数.由题意列出方程ax＋b＋c＝x,(1－a)x＝b＋c，x＝．

请你将(1)b＝4，c＝38，a＝；(2)b＝6，c＝22，a＝；(3)b＝2，c=19，a＝分别代入x＝，计算一下x的值是否与第一个、第二个大臣算出的珍珠数相符?并请你为波斯国王当一回“参谋”，三个大臣该如何得到国王的悬赏？

查看答案和解析>>

科目：初中数学 来源：2012-2013学年江西省吉安市朝宗实验学校七年级下学期第一次段考数学试卷（带解析） 题型：解答题

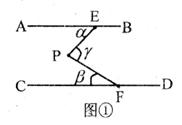
如图所示，平面内，AB∥CD，点E、F分别在直线AB、CD上，点P是这两条直线外的一个动点，连接EP、FP，设∠AEP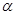＝∠，∠CFP＝∠，∠EPF＝∠。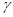

（1）如果点P在直线AB、CD之间，那么∠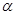、∠、∠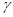之间有怎样的数量关系（以图①为例）？并说明理由。
（2）在（1）中的条件下，请画出符合条件的其他图形（每一种位置只画一个示意图），并直接写出∠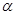、∠、∠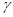之间的数量关系。（提示：对点P与直线EF的位置关系进行讨论）
（3）如果点P在直线AB上方，请画出所有符合题意的图形（每一种位置只画一个示意图），并探索∠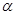、∠、∠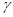之间的数量关系，选一种图形说明理由。

查看答案和解析>>

科目：初中数学 来源：2015届江西省七年级下学期第一次段考数学试卷（解析版） 题型：解答题

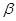如图所示，平面内，AB∥CD，点E、F分别在直线AB、CD上，点P是这两条直线外的一个动点，连接EP、FP，设∠AEP＝∠，∠CFP＝∠，∠EPF＝∠。

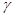（1）如果点P在直线AB、CD之间，那么∠、∠、∠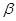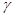之间有怎样的数量关系（以图①为例）？并说明理由。

（2）在（1）中的条件下，请画出符合条件的其他图形（每一种位置只画一个示意图），并直接写出∠、∠、∠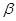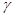之间的数量关系。（提示：对点P与直线EF的位置关系进行讨论）

（3）如果点P在直线AB上方，请画出所有符合题意的图形（每一种位置只画一个示意图），并探索∠、∠、∠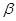之间的数量关系，选一种图形说明理由。

查看答案和解析>>

科目：初中数学 来源： 题型：

如图，在平行四边形ABCD中，AB＝5，BC＝10，F为AD的中点，CE⊥AB于E，设∠ABC＝α(60°≤α＜90°)．

(1)当α＝60°时，求CE的长；

(2)当60°＜α＜90°时，

①是否存在正整数k，使得∠EFD＝k∠AEF？若存在，求出k的值；若不存在，请说明理由．

②连接CF，当CE²－CF²取最大值时，求tan∠DCF的值．

分析　(1)利用60°角的正弦值列式计算即可得解；

(2)①连接CF并延长交BA的延长线于点G，利用“角边角”证明△AFG和△CFD全等，根据全等三角形对应边相等可得CF＝GF，AG＝CD，再利用直角三角形斜边上的中线等于斜边的一半可得EF＝GF，再根据AB、BC的长度可得AG＝AF，然后利用等边对等角的性质可得∠AEF＝∠G＝∠AFG，根据三角形的一个外角等于与它不相邻的两个内角的和可得∠EFC＝2∠G，然后推出∠EFD＝3∠AEF，从而得解；