练习册

  • 练习册
  • 试题
    精英家教网 > 初中数学 > 题目详情

    对参加某次野外训练的中学生的年龄（单位：岁）进行统计，结果如表：

    年龄

    13

    14

    15

    16

    17

    18

    人数

    4

    5

    6

    6

    7

    2

    则这些学生年龄的众数和中位数分别是（　　）

    　

    A．

    17，15.5

    B．

    17，16

    C．

    15，15.5

    D．

    16，16


    A

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：初中数学 来源： 题型：


    化简：﹣=　　．

    查看答案和解析>>

    科目：初中数学 来源： 题型：


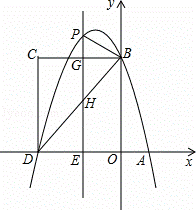
    如图，在平面直角坐标系中，抛物线y=﹣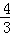x2+bx+c与x轴交于A、D两点，与y轴交于点B，四边形OBCD是矩形，点A的坐标为（1，0），点B的坐标为（0，4），已知点E（m，0）是线段DO上的动点，过点E作PE⊥x轴交抛物线于点P，交BC于点G，交BD于点H．

    （1）求该抛物线的解析式；

    （2）当点P在直线BC上方时，请用含m的代数式表示PG的长度；

    （3）在（2）的条件下，是否存在这样的点P，使得以P、B、G为顶点的三角形与△DEH相似？若存在，求出此时m的值；若不存在，请说明理由．

    查看答案和解析>>

    科目：初中数学 来源： 题型：


    化简：（a+b）（a﹣b）+2b2．

    查看答案和解析>>

    科目：初中数学 来源： 题型：


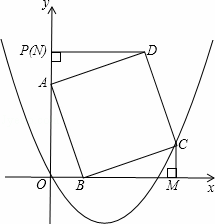
    如图，在平面直角坐标系中，已知点P（0，4），点A在线段OP上，点B在x轴正半轴上，且AP=OB=t，0＜t＜4，以AB为边在第一象限内作正方形ABCD；过点C、D依次向x轴、y轴作垂线，垂足为M，N，设过O，C两点的抛物线为y=ax2+bx+c．

    （1）填空：△AOB≌△　      　≌△BMC（不需证明）；用含t的代数式表示A点纵坐标：A（0，　    　）；

    （2）求点C的坐标，并用含a，t的代数式表示b；

    （3）当t=1时，连接OD，若此时抛物线与线段OD只有唯一的公共点O，求a的取值范围；

    （4）当抛物线开口向上，对称轴是直线x=2﹣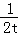，顶点随着的增大向上移动时，求t的取值范围．

    查看答案和解析>>

    科目：初中数学 来源： 题型：


    如图，在△ABC中，D、E分别是AB、BC上的点，且DE∥AC，若S△BDE：S△CDE=1：4，则S△BDE：S△ACD=（　　）

    　

    A．

    1：16

    B．

    1：18

    C．

    1：20

    D．

    1：24

    查看答案和解析>>

    科目：初中数学 来源： 题型：


    如图在坐标系中放置一菱形OABC，已知∠ABC=60°，OA=1．先将菱形OABC沿x轴的正方向无滑动翻转，每次翻转60°，连续翻转2014次，点B的落点依次为B1，B2，B3，…，则B2014的坐标为　　．

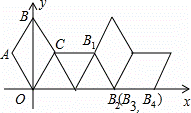
    查看答案和解析>>

    科目：初中数学 来源： 题型：


    如图，正方形ABCD的边CD与正方形CGEF的边CE重合，O是EG的中点，∠EGC的评分项GH过点D，交BE于H，连接OH、FH、EG与FH交于M，对于下面四个结论：

    ①GH⊥BE；②HOBG；③点H不在正方形CGFE的外接圆上；④△GBE∽△GMF．

    其中正确的结论有（　　）

    　

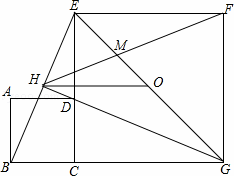
    A．

    1个

    B．

    2个

    C．

    3个

    D．

    4个

    查看答案和解析>>

    科目：初中数学 来源： 题型：


    如图，在平面直角坐标中，点O为坐标原点，直线y=﹣x+4与x轴交于点A，过点A的抛物线y=ax2+bx与直线y=﹣x+4交于另一点B，且点B的横坐标为1．

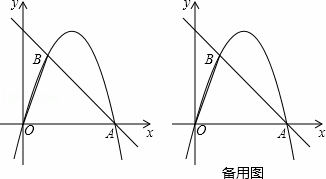
    （1）求a，b的值；

    （2）点P是线段AB上一动点（点P不与点A、B重合），过点P作PM∥OB交第一象限内的抛物线于点M，过点M作MC⊥x轴于点C，交AB于点N，过点P作PF⊥MC于点F，设PF的长为t，MN的长为d，求d与t之间的函数关系式（不要求写出自变量t的取值范围）；

    （3）在（2）的条件下，当S△ACN=S△PMN时，连接ON，点Q在线段BP上，过点Q作QR∥MN交ON于点R，连接MQ、BR，当∠MQR﹣∠BRN=45°时，求点R的坐标．

    查看答案和解析>>

    同步练习册答案