
【题目】如图,在△ABC中,已知AB=AC,D、E、B、C在同一条直线上,且AB2=BDCE,求证:△ABD∽△ECA.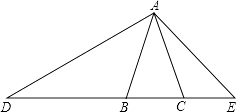
科目:初中数学 来源: 题型:
【题目】已知:在△ABC中,∠ACB=90°,点P是线段AC上一点,过点A作AB的垂线,交BP的延长线于点M,MN⊥AC于点N,PQ⊥AB于点Q,AQ=MN. 求证:
(1)△APM是等腰三角形;
(2)PC=AN.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在△ABC中,AB=AC,∠BAC=50°,∠BAC的平分线与AB的中垂线交于点O,点C沿EF折叠后与点O重合,则∠CEO的度数是_____.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在△ABC中,AB≠AC.D、E分别为边AB、AC上的点.AC=3AD,AB=3AE,点F为BC边上一点,添加一个条件: , 可以使得△FDB与△ADE相似.(只需写出一个) 
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】今年南方某地发生特大洪灾,政府为了尽快搭建板房安置灾民,给某厂下达了生产A种板材48000㎡和B种板材24000㎡的任务.
⑴如果该厂安排210人生产这两种材,每人每天能生产A种板材60㎡或B种板材40㎡,请问:应分
别安排多少人生产A种板材和B种板材,才能确保同时完成各自的生产任务?
⑵某灾民安置点计划用该厂生产的两种板材搭建甲、乙两种规格的板房共400间,已知建设一间甲型板房和一间乙型板房所需板材及安置人数如下表所示:
板房 | A种板材(m2) | B种板材(m2) | 安置人数 |
甲型 | 108 | 61 | 12 |
乙型 | 156 | 51 | 10 |
问这400间板房最多能安置多少灾民?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某超市的某种商品一周内每天的进价与售价信息和实际每天的销售量情况如图表所示:
进价与售价折线图(单位:元/斤)

实际销售量表(单位:斤)
日期 | 周一 | 周二 | 周三 | 周四 | 周五 | 周六 | 周日 |
销售量 | 30 | 40 | 35 | 30 | 50 | 60 | 50 |
则下列推断不合理的是( )
A. 该商品周一的利润最小
B. 该商品周日的利润最大
C. 由一周中的该商品每天售价组成的这组数据的众数是4(元/斤)
D. 由一周中的该商品每天进价组成的这组数据的中位数是3(元/斤)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】数据x1,x2,…,xn的方差为A,则数据3x1+1,3x2+1,…3xn+1的方差为( )
A. 3A B. 3A+1 C. 9A D. 9A+1
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com