
【题目】如图,抛物线y=ax2+2ax+c的图象与x轴交于A、B两点(点A在点B的左边)AB=4,与y轴交于点C,OC=OA,点D为抛物线的顶点. 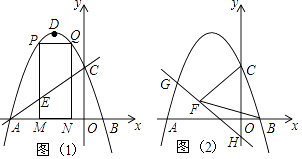
(1)求抛物线的解析式;
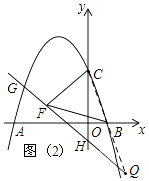
(2)点M(m,0)为线段AB上一点(点M不与点A、B重合),过点M作x轴的垂线,与直线AC交于点E,与抛物线交于点P,过点P作PQ∥AB交抛物线于点Q,过点Q作QN⊥x轴于点N,可得矩形PQNM,如图1,点P在点Q左边,当矩形PQNM的周长最大时,求m的值,并求出此时的△AEM的面积;
(3)已知H(0,﹣1),点G在抛物线上,连HG,直线HG⊥CF,垂足为F,若BF=BC,求点G的坐标.
【答案】
(1)解:由抛物线y=ax2+2ax+c,可得C(0,c),对称轴为x=﹣ ![]() =﹣1,
=﹣1,
∵OC=OA,
∴A(﹣c,0),B(﹣2+c,0),
∵AB=4,
∴﹣2+c﹣(﹣c)=4,
∴c=3,
∴A(﹣3,0),
代入抛物线y=ax2+2ax+3,得
0=9a﹣6a+3,
解得a=﹣1,
∴抛物线的解析式为y=﹣x2﹣2x+3
(2)解:如图1,∵M(m,0),PM⊥x轴,
∴P(m,﹣m2﹣2m+3),
又∵对称轴为x=﹣1,PQ∥AB,
∴Q(﹣2﹣m,﹣m2﹣2m+3),
又∵QN⊥x轴,
∴矩形PQNM的周长
=2(PM+PQ)
=2[(﹣m2﹣2m+3)+(﹣2﹣m﹣m)]
=2(﹣m2﹣4m+1)
=﹣2(m+2)2+10,
∴当m=﹣2时,矩形PQNM的周长有最大值10,
此时,M(﹣2,0),
由A(﹣3,0),C(0,3),可得
直线AC为y=x+3,AM=1,
∴当x=﹣2时,y=1,即E(﹣2,1),ME=1,
∴△AEM的面积= ![]() ×AM×ME=
×AM×ME= ![]() ×1×1=
×1×1= ![]()
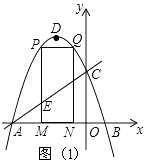
(3)解:如图2,连接CB并延长,交直线HG与Q,
∵HG⊥CF,BC=BF,
∴∠BFC+∠BFQ=∠BCF+∠Q=90°,∠BFC=∠BCF,
∴∠BFQ=∠Q,
∴BC=BF=BQ,
又∵C(0,3),B(1,0),
∴Q(2,﹣3),
又∵H(0,﹣1),
∴QH的解析式为y=﹣x﹣1,
解方程组 ![]() ,可得
,可得
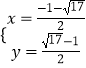 或
或 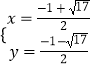 ,
,
∴点G的坐标为( ![]() ,
, ![]() )或(
)或( ![]() ,
, ![]() ).
).
【解析】(1)根据抛物线y=ax2+2ax+c,可得C(0,c),对称轴为x﹣1,再根据OC=OA,AB=4,可得A(﹣3,0),最后代入抛物线y=ax2+2ax+3,得抛物线的解析式为y=﹣x2﹣2x+3;(2)根据点M(m,0),可得矩形PQNM中,P(m,﹣m2﹣2m+3),Q(﹣2﹣m,﹣m2﹣2m+3),再根据矩形PQNM的周长=2(PM+PQ)=﹣2(m+2)2+10,可得当m=﹣2时,矩形PQNM的周长有最大值10,M的坐标为(﹣2,0),最后由直线AC为y=x+3,AM=1,求得E(﹣2,1),ME=1,据此求得△AEM的面积;(3)连接CB并延长,交直线HG与Q,根据已知条件证明BC=BF=BQ,再根据C(0,3),B(1,0),得出Q(2,﹣3),根据H(0,﹣1),求得QH的解析式为y=﹣x﹣1,最后解方程组 ![]() ,可得点G的坐标.
,可得点G的坐标.
【考点精析】本题主要考查了二次函数的最值和矩形的性质的相关知识点,需要掌握如果自变量的取值范围是全体实数,那么函数在顶点处取得最大值(或最小值),即当x=-b/2a时,y最值=(4ac-b2)/4a;矩形的四个角都是直角,矩形的对角线相等才能正确解答此题.


 名校课堂系列答案
名校课堂系列答案科目:初中数学 来源: 题型:
【题目】若我们规定三角“![]() ”表示为:abc;方框“
”表示为:abc;方框“![]() ”表示为:(xm+yn).例如:
”表示为:(xm+yn).例如:![]() =1×19×3÷(24+31)=3.请根据这个规定解答下列问题:
=1×19×3÷(24+31)=3.请根据这个规定解答下列问题:
(1)计算:![]() = ______ ;
= ______ ;
(2)代数式 为完全平方式,则k= ______ ;
为完全平方式,则k= ______ ;
(3)解方程:![]() =6x2+7.
=6x2+7.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系内,点O为坐标原点,点A在x轴负半轴上,点B、C分别在x轴、y轴正半轴上,且OB=2OA,OBOC=OCOA=2.
(1)求点C的坐标;
(2)点P从点A出发以每秒1个单位的速度沿AB向点B匀速运动,同时点Q从点B出发以每秒3个单位的速度沿BA向终点A匀速运动,当点Q到达终点A时,点P、Q均停止运动,设点P运动的时间为t(t>0)秒,线段PQ的长度为y,用含t的式子表示y,并写出相应的t的范围;
(3)在(2)的条件下,过点P作x轴的垂线PM,PM=PQ,是否存在t值使点O为PQ中点? 若存在求t值并求出此时△CMQ的面积.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在甲、乙两名同学中选拔一人参加“中华好诗词”大赛,在相同的测试条件下,两人5次测试成绩(单位:分)如下:
甲:79,86,82,85,83
乙:88,79,90,81,72.
回答下列问题:
(1)甲成绩的平均数是______ ,乙成绩的平均数是______ ;
(2)经计算知S甲2=6,S乙2=42.你认为选拔谁参加比赛更合适,说明理由;
(3)如果从甲、乙两人5次的成绩中各随机抽取一次成绩进行分析,求抽到的两个人的成绩都大于80分的概率.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】下列说法中错误的是( )
A. 在△ABC中,∠C=∠A-∠B,则△ABC为直角三角形
B. 在△ABC中,若∠A∶∠B∶∠C=5∶2∶3,则△ABC为直角三角形
C. 在△ABC中,若a=![]() c,b=
c,b=![]() c,则△ABC为直角三角形
c,则△ABC为直角三角形
D. 在△ABC中,若a∶b∶c=2∶2∶4,则△ABC为直角三角形
查看答案和解析>>
科目:初中数学 来源: 题型:
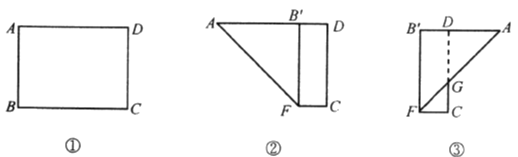
【题目】如图①,在长方形![]() 中,
中,![]() cm,
cm,![]() cm.现将其按下列步骤折叠:(1)将边
cm.现将其按下列步骤折叠:(1)将边![]() 向边
向边![]() 折叠,使边
折叠,使边![]() 落在边
落在边![]() 上,得到折痕
上,得到折痕![]() ,如图②;(2)将
,如图②;(2)将![]() 沿
沿![]() 折叠,
折叠,![]() 与
与![]() 交于点
交于点![]() ,如图③.则所得梯形
,如图③.则所得梯形![]() 的周长等于( )
的周长等于( )
A. ![]() cm B.
cm B. ![]() cm
cm
C. ![]() cm D.
cm D. ![]() cm
cm
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,△ABC和△EBD中,∠ABC=∠DBE=90°,AB=CB,BE=BD,连接AE,CD,AE与CD交于点M,AE与BC交于点N.
(1)求证:AE=CD;
(2)求证:AE⊥CD;
(3)连接BM,有以下两个结论:①BM平分∠CBE;②MB平分∠AMD.其中正确的有 (请写序号,少选、错选均不得分).

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com