
分析 (1)由平行四边形、矩形、菱形、正方形的性质即可得出结论;
(2)四边形ABCD的面积=△ABC的面积+△ADC的面积=$\frac{1}{2}$AC•BO+$\frac{1}{2}$AC•DO=$\frac{1}{2}$AC•BD;
(3)①连接CG、BE,证出∠GAB=∠CAE,由SAS证明△GAB≌△CAE,得出BG=CE,∠ABG=∠AEC,再由角的互余关系和三角形内角和定理求出∠BNM=90°,得出BG⊥CE即可;
②根据垂美四边形的性质、勾股定理、结合(2)的结论计算即可.
解答 (1)解:∵在平行四边形、矩形、菱形、正方形中,两条对角线互相垂直的四边形是菱形、正方形,
∴菱形和正方形一定是垂美四边形;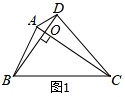
故答案为:菱形、正方形;
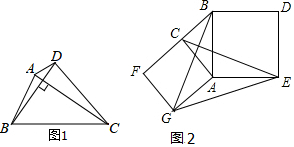
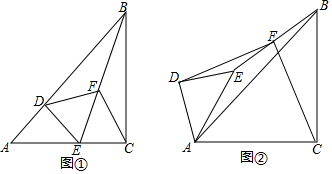
(2)解:如图1所示:
∵四边形ABCD的面积=△ABC的面积+△ADC的面积=$\frac{1}{2}$AC•BO+$\frac{1}{2}$AC•DO=$\frac{1}{2}$AC(BO+DO)=$\frac{1}{2}$AC•BD;
故答案为:$\frac{1}{2}$AC•BD;
(3)①证明:连接CG、BE,如图2所示: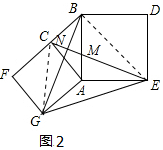
∵四边形ACFG和四边形ABDE是正方形,
∴∠F=∠CAG=∠BAE=90°,FG=AG=AC=CF,AB=AE,
∴∠CAG+∠BAC=∠BAE+∠BAC,
即∠GAB=∠CAE,
在△GAB和△CAE中,$\left\{\begin{array}{l}{AG=AC}&{\;}\\{∠GAB=∠CAE}&{\;}\\{AB=AE}&{\;}\end{array}\right.$,
∴△GAB≌△CAE(SAS),
∴BG=CE,∠ABG=∠AEC,
又∵∠AEC+∠AME=90°,∠AME=∠BMN,
∴∠ABG+∠BMN=90°,
∴∠BNM=90°,
∴BG⊥CE,
∴四边形BCGE为垂美四边形;
②解:∵FG=CF=AC=4,∠ACB=90°,AB=5,
∴BC=$\sqrt{A{B}^{2}-A{C}^{2}}$=3,
∴BF=BC+CF=7,
在Tt△BFG中,BG=$\sqrt{B{F}^{2}+F{G}^{2}}$=$\sqrt{{7}^{2}+{4}^{2}}$=$\sqrt{65}$,
∴CE=BG=$\sqrt{65}$,
∵四边形BCGE为垂美四边形,
∴四边形BCGE的面积=$\frac{1}{2}$BG•CE=$\frac{65}{2}$.
点评 本题是四边形综合题目,考查的是垂美四边形的判定与性质、正方形的性质、全等三角形的判定和性质、垂直的定义、勾股定理的应用,正确理解垂美四边形的定义、灵活运用勾股定理是解题的关键.


 目标测试系列答案
目标测试系列答案科目:初中数学 来源: 题型:解答题
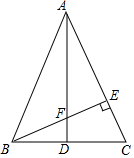 如图,△ABC中,AB=AC,AD是∠BAC的平分线,交BC于D,过点B作BE⊥AC于E,交AD于F,又知AF=2BD,△BCE与△AFE全等吗?为什么?
如图,△ABC中,AB=AC,AD是∠BAC的平分线,交BC于D,过点B作BE⊥AC于E,交AD于F,又知AF=2BD,△BCE与△AFE全等吗?为什么?查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 向左平移5单位 | B. | 向左平移3单位 | C. | 向右平移1单位 | D. | 向右平移2单位 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 为了了解大气污染情况,某学校兴趣小组搜集了2017年上半年中120天郑州市的空气质量指数,绘制了如下不完整的统计图表:
为了了解大气污染情况,某学校兴趣小组搜集了2017年上半年中120天郑州市的空气质量指数,绘制了如下不完整的统计图表:| 级别 | 指数 | 天数 | 百分比 |
| 优 | 0-50 | 24 | m |
| 良 | 51-100 | a | 40% |
| 轻度污染 | 101-150 | 18 | 15% |
| 中度污染 | 151-200 | 15 | 12.5% |
| 重度污染 | 201-300 | 9 | 7.5% |
| 严重污染 | 大于300 | 6 | 5% |
| 合计 | 120 | 100% |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
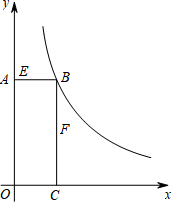 如图,矩形AOCB的顶点B在反比例函数$y=\frac{k}{x}(k>0$,x>0)的图象上,且AB=3,BC=8.若动点E从A开始沿AB向B以每秒1个单位长度的速度运动,同时动点F从B开始沿BC向C以每秒2个单位长度的速度运动,当其中一个动点到达端点时,另一个动点随之停止运动,设运动时间为t秒.
如图,矩形AOCB的顶点B在反比例函数$y=\frac{k}{x}(k>0$,x>0)的图象上,且AB=3,BC=8.若动点E从A开始沿AB向B以每秒1个单位长度的速度运动,同时动点F从B开始沿BC向C以每秒2个单位长度的速度运动,当其中一个动点到达端点时,另一个动点随之停止运动,设运动时间为t秒.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com