
分析 用各队10次数据相加求出和,再除以10即可求出平均数;
根据方差公式进行计算出结果即可.
解答 解:甲队平均分$\overline{{x}_{甲}}$=(100+97+99+96+102+103+104+101+101+100)÷10=100.3,
乙队平均分$\overline{{x}_{乙}}$=(97+97+99+95+102+100+104+104+103+102)÷10=100.3,
甲队方差${S}_{甲}^{2}$=$\frac{1}{10}$[(100-100.3)2+(97-100.3)2+…+(100-100.3)2]=5.49
乙队方差${S}_{乙}^{2}$=$\frac{1}{10}$[(97-100.3)2+(97-100.3)2+…+(102-100.3)2]=9.21,
甲方差小于乙方差,
甲队在比赛中的成绩较为稳定.
点评 本题考查了方差,用到的知识点是方差、中位数和众数,方差是用来衡量一组数据波动大小的量,方差越大,表明这组数据偏离平均数越大,即波动越大,数据越不稳定;反之,方差越小,表明这组数据分布比较集中,各数据偏离平均数越小,即波动越小,数据越稳定.


 口算题卡北京妇女儿童出版社系列答案
口算题卡北京妇女儿童出版社系列答案科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
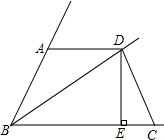 如图,已知点D在∠ABC内部,DE⊥BC,垂足为E,∠BAD+∠BCD=180°.
如图,已知点D在∠ABC内部,DE⊥BC,垂足为E,∠BAD+∠BCD=180°.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
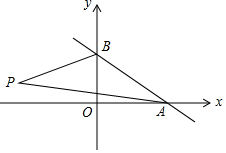 如图,已知直线l1经过点A(2,0)与点B(0,1),如果在第二象限内有一点P(a,$\frac{1}{2}$),且△APB的面积为3,求a的值.
如图,已知直线l1经过点A(2,0)与点B(0,1),如果在第二象限内有一点P(a,$\frac{1}{2}$),且△APB的面积为3,求a的值.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com