
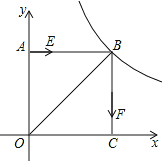
【题目】如图,正方形AOCB在平面直角坐标系xoy中,点O为原点,点B在反比例函数![]() (x>0)图象上,△BOC的面积为8.
(x>0)图象上,△BOC的面积为8.
(1)求反比例函数![]() 的关系
的关系
(2)若动点E从A开始沿AB向B以每秒1个单位的速度运动,同时动点F从B开始沿BC向C以每秒2个单位的速度运动,当其中一个动点到达端点时,另一个动点随之停止运动.若运动时间用t表示,△BEF的面积用S表示,求出S关于t的函数关系式?
(3)当运动时间为![]() 秒时,在坐标轴上是否存在点P,使△PEF的周长最小?若存在,请求出点P的坐标;若不存在,请说明理由.
秒时,在坐标轴上是否存在点P,使△PEF的周长最小?若存在,请求出点P的坐标;若不存在,请说明理由.
【答案】(1)、y=![]() ;(2)、S=-
;(2)、S=-![]() +4;(3)、P(
+4;(3)、P(![]() ,0)
,0)
【解析】
试题分析:(1)、设点B的坐标为(a,a),根据三角形的面积得出a的值,然后求出点B的坐标,计算反比例函数的解析式;(2)、根据题意得出AE=t,BF=2t,BE=4-t,然后求出函数解析式;(3)、首先根据t的值求出点E和点F的坐标,作F点关于x轴的对称点![]() ,求出直线E
,求出直线E![]() 的直线解析式,从而得出点P的坐标.
的直线解析式,从而得出点P的坐标.
试题解析:(1)、∵四边形AOCB为正方形,
∴AB=BC=OC=OA,
设点B坐标为(a,a),
∵![]() C=8,
C=8,
∴![]() =8,
=8,
∴a=±4
又∵点B在第一象限,
∴点B坐标为(4,4),
将点B(4,4)代入y=![]() 得,k=16
得,k=16
∴反比例函数解析式为y=![]()
(2)、∵运动时间为t,
∴AE=t,BF=2t
∵AB=4,
∴BE=4-t,
∴![]() =
=![]() (4-t)2t=-
(4-t)2t=-![]() +4t=--
+4t=--![]() +4,
+4,
(3)、存在.
当t=![]() 时,点E的坐标为(
时,点E的坐标为(![]() ,4),点F的坐标为(4,
,4),点F的坐标为(4,![]() )
)
作F点关于x轴的对称点![]() ,得F1(4,-
,得F1(4,-![]() ),经过点E、
),经过点E、![]() 作直线
作直线
由E(![]() ,4),
,4),![]() (4,-
(4,-![]() )代入y=ax+b得:
)代入y=ax+b得:
解得:
可得直线E![]() 的解析式是y=-2x+
的解析式是y=-2x+![]()
当y=0时,x=![]()
∴P点的坐标为(![]() ,0)
,0)



 新卷王期末冲刺100分系列答案
新卷王期末冲刺100分系列答案 全能闯关100分系列答案
全能闯关100分系列答案科目:初中数学 来源: 题型:
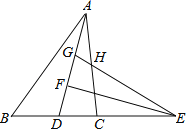
【题目】如图,在△ABC中,5AB=6AC,AD为△ABC的角平分线,点E在BC的延长线上,EF⊥AD于点F,点G在AF上,FG=FD,连接EG交AC于点H.若点H是AC的中点,则![]() 的值为 .
的值为 .
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】中国科学家屠呦呦获得了诺贝尔生理学或医学奖,她研发的抗疟新药每年能为近120万婴幼儿免除疟疾的危害.其中120万用科学记数法表示为( )
A.12×103
B.1.2×104
C.1.2×106
D.1.2×108
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】观察下列一组图形中点的个数,其中第1个图中共有4个点,第2个图中共有10个点,第3个图中共有19个点,…按此规律第7个图中共有点的个数是( )

A.46 B.85 C.72 D.66
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】二次函数y=ax2+bx+c(a≠0)的图象如图所示,其对称轴为x=1,下列结论中错误的是( )
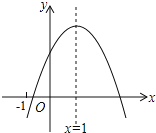
A.abc<0 B.2a+b=0 C.b2﹣4ac>0 D.a﹣b+c>0
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】小张五次数学考试成绩分别为:86分、78分、80分、85分、92分,李老师想了解小张数学成绩波动情况,则李老师最关注小张数学成绩的( )
A.方差
B.众数
C.中位数
D.平均数
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在信宜市某“三华李”种植基地有A、B两个品种的树苗出售,已知A种比B种每株多2元,买1株A种树苗和2株B种树苗共需20元.
(1)问A、B两种树苗每株分别是多少元?
(2)为扩大种植,某农户准备购买A、B两种树苗共360株,且A种树苗数量不少于B种数量的一半,请求出费用最省的购买方案.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com