
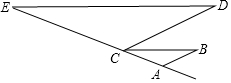
 已知:如图,AB∥CD,∠B=∠D,求证:∠E=∠BCA
已知:如图,AB∥CD,∠B=∠D,求证:∠E=∠BCA 轻松课堂单元期中期末专题冲刺100分系列答案
轻松课堂单元期中期末专题冲刺100分系列答案科目:初中数学 来源: 题型:选择题
| A. | $\sqrt{2}$-2$\sqrt{2}$=-$\sqrt{2}$ | B. | $\sqrt{8{a}^{2}}$=4a(a>0) | C. | $\sqrt{(-4)×(-9)}$=$\sqrt{-4}$×$\sqrt{-9}$ | D. | $\sqrt{6}$÷$\sqrt{3}$=$\sqrt{3}$ |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | -$\frac{8}{x-2}$ | B. | $\frac{8}{x-2}$ | C. | $\frac{8}{x+2}$ | D. | -$\frac{8}{x+2}$ |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
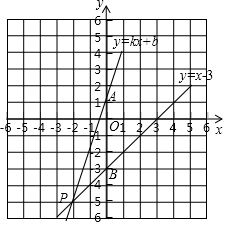 如图,已知一次函数y=kx+b经过点A(0,1)且和直线y=x-3交于点P(a,-5).
如图,已知一次函数y=kx+b经过点A(0,1)且和直线y=x-3交于点P(a,-5).查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
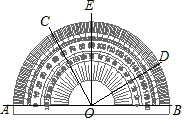 如图所示,用量角器度量几个角的度数.下列结论中正确的是( )
如图所示,用量角器度量几个角的度数.下列结论中正确的是( )| A. | ∠BOC=60° | B. | ∠COA是∠EOD的余角 | ||
| C. | ∠AOC=∠BOD | D. | ∠AOD与∠COE互补 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com