
【题目】如果两个三角形的两条边对应相等,夹角互补,那么这两个三角形叫做互补三角形,如图2,分别以△ABC的边AB、AC为边向外作正方形ABDE和ACGF,则图中的两个三角形就是互补三角形.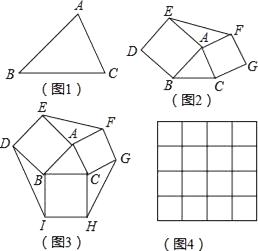
(1)用尺规将图1中的△ABC分割成两个互补三角形;
(2)证明图2中的△ABC与△AEF两个互补三角形面积相等;
(3)如图3,在图2的基础上再以BC为边向外作正方形BCHI.
①已知三个正方形面积分别是17、13、10,在如图4的网格中(网格中每个小正方形的边长为1)画出边长为 ![]() 、
、 ![]() 、
、 ![]() 的三角形,并计算图3中六边形DEFGHI的面积.
的三角形,并计算图3中六边形DEFGHI的面积.
②若△ABC的面积为2,求以EF、DI、HG的长为边的三角形面积.
【答案】
(1)解:如图1中,作BC边上的中线AD,△ABD和△ADC是互补三角形.
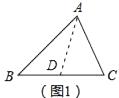
(2)解:如图2中,延长FA到点H,使得AH=AF,连接EH.

∵四边形ABDE,四边形ACGF是正方形,
∴AB=AE,AF=AC,∠BAE=∠CAF=90°,
∴∠EAF+∠BAC=180°,
∴△AEF和△ABC是两个互补三角形.
∵∠EAH+∠HAB=∠BAC+∠HAB=90°,
∴∠EAH=∠BAC,
∵AF=AC,
∴AH=AC,
在△AEH和△ABC中,
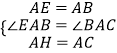
∴△AEH≌△ABC,
∴S△AEF=S△AEH=S△ABC.
(3)解:①边长为 ![]() 、
、 ![]() 、
、 ![]() 的三角形如图4所示.
的三角形如图4所示.

∵S△ABC=3×4﹣2﹣1.5﹣3=5.5,
∴S六边形=17+13+10+4×5.5=62.
②如图3中,平移△CHG到AMF,连接EM,IM,则AM=CH=BI,设∠ABC=x,

∵AM∥CH,CH⊥BC,
∴AM⊥BC,
∴∠EAM=90°+90°﹣x=180°﹣x,
∵∠DBI=360°﹣90°﹣90°﹣x=180°﹣x,
∴∠EAM=∠DBI,∵AE=BD,
∴△AEM≌△DBI,
∵在△DBI和△ABC中,DB=AB,BI=BC,∠DBI+∠ABC=180°,
∴△DBI和△ABC是互补三角形,
∴S△AEM=S△AEF=S△AFM=2,
∴S△EFM=3S△ABC=6.
【解析】(1)作BC边上的中线AD,根据三角形中线的定义知BD=CD,AD=AD,根据领补角的定义![]() +
+![]() =180
=180![]() ,根据互补三角形的定义△ABD和△ADC是互补三角形;
,根据互补三角形的定义△ABD和△ADC是互补三角形;
(2)延长FA到点H,使得AH=AF,连接EH.根据正方形的性质AB=AE,AF=AC,∠BAE=∠CAF=90°,根据周角的定义知∠EAF+∠BAC=180°,根据互补三角形的定义得出△AEF和△ABC是两个互补三角形,根据同角的余角相等得出∠EAH=∠BAC,根据正方形的性质及作的辅助线知AH=AC,进而利用SAS判断出△AEH≌△ABC,从而根据全等三角形的面积相等得出S△AEH=S△ABC,由根据等底同高的两个三角形面积相等得出S△AEF=S△AEH,从而得出S△AEF=S△AEH=S△ABC;
(3)①利用勾股定理,结合网格结构画出边长为![]() ,
,![]() ,
,![]() 的三角形即可;利用割补法求面积即可;②如图3中,平移△CHG到AMF,连接EM,IM,则AM=CH=BI,设∠ABC=x,根据平行线的性质得出AM⊥BC,根据垂直的定义得出∠EAM=90°+90°﹣x=180°﹣x,根据周角的定义,及等量代换得出∠EAM=∠DBI,从而判断出△AEM≌△DBI,在△DBI和△ABC中,DB=AB,BI=BC,∠DBI+∠ABC=180°,根据互补三角形的定义知△DBI和△ABC是互补三角形,然后得出结论。
的三角形即可;利用割补法求面积即可;②如图3中,平移△CHG到AMF,连接EM,IM,则AM=CH=BI,设∠ABC=x,根据平行线的性质得出AM⊥BC,根据垂直的定义得出∠EAM=90°+90°﹣x=180°﹣x,根据周角的定义,及等量代换得出∠EAM=∠DBI,从而判断出△AEM≌△DBI,在△DBI和△ABC中,DB=AB,BI=BC,∠DBI+∠ABC=180°,根据互补三角形的定义知△DBI和△ABC是互补三角形,然后得出结论。
【考点精析】掌握三角形的面积和正方形的性质是解答本题的根本,需要知道三角形的面积=1/2×底×高;正方形四个角都是直角,四条边都相等;正方形的两条对角线相等,并且互相垂直平分,每条对角线平分一组对角;正方形的一条对角线把正方形分成两个全等的等腰直角三角形;正方形的对角线与边的夹角是45o;正方形的两条对角线把这个正方形分成四个全等的等腰直角三角形.


 小学生10分钟口算测试100分系列答案
小学生10分钟口算测试100分系列答案科目:初中数学 来源: 题型:
【题目】在平面直角坐标系中,O为原点,边长为2的正方形OABC的两顶点A、C分别在y轴、x轴的正半轴上,现将正方形OABC绕点O顺时针旋转.
(1)如图①,当点A的对应的A′落在直线y=x上时,点A′的对应坐标为;点B的对应点B′的坐标为;
(2)旋转过程中,AB边交直线y=x于点M,BC边交x轴于点N,当A点第一次落在直线y=x上时,停止旋转.
①如图2,在正方形OABC旋转过程中,线段AM,MN,NC三者满足什么样的数量关系?请说明理由;
②当AC∥MN时,求△MBN内切圆的半径(直接写出结果即可)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在每个小正方形的边长为1的网格中,点A、点B均为格点.
(1)AB的长等于;
(2)若点C是以AB为底边的等腰直角三角形的顶点,点D在边AC上,且满足S△ABD= ![]() S△ABC . 请在如图所示的网格中,用无刻度的直尺,画出线段BD,并简要说明点D的位置时如何找到的(不要求证明). .
S△ABC . 请在如图所示的网格中,用无刻度的直尺,画出线段BD,并简要说明点D的位置时如何找到的(不要求证明). .
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】观察下列等式:
第一个等式: ![]()
第二个等式: ![]()
第三个等式: ![]()
第四个等式: ![]()
则式子![]() __________________;
__________________;
用含n的代数式表示第n个等式: ![]() ____________________________;
____________________________;
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】下表是小华做观察水的沸腾实验时所记录的数据:

(1)时间是8分钟时,水的温度为_____;
(2)此表反映了变量_____和_____之间的关系,其中_____是自变量,_____是因变量;
(3)在_____时间内,温度随时间增加而增加;_____时间内,水的温度不再变化.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】甲、乙两台机床同时生产同一种零件,在10天中两台机床每天生产的次品数如下:
甲:0,1,0,2,2,0,3,1,2,4;
乙:2,3,1,1,0,2,1,1,0,1.
(1)分别计算两组数据的平均数和方差;
(2)从结果看,在10天中哪台机床出现次品的波动较小?
(3)由此推测哪台机床的性能较好
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】(7分)某学校举行演讲比赛,选出了10名同学担任评委,并事先拟定从如下4个方案中选择合理的方案来确定每个演讲者的最后得分(满分为10分):
方案1:所有评委所给分的平均数,
方案2:在所有评委所给分中,去掉一个最高分和一个最低分.然后再计算其余给分的l平均数.
方案3:所有评委所给分的中位效.
方案4:所有评委所给分的众数.
为了探究上述方案的合理性.先对某个同学的演讲成绩进行了统计实验.下面是这个同学的得分统计图:

(1)分别按上述4个方案计算这个同学演讲的最后得分;
(2)根据(1)中的结果,请用统计的知识说明哪些方案不适台作为这个同学演讲的最后得分,并给出该同学的最后得分.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】2016年宁波市北仑区体育中考的3个选测项目分别是50米跑,一分钟跳绳,篮球运球投篮.另规定:游泳满分的学生,只需从3个选测项目中选择一项进行测试;游泳未得满分或未参加的学生,需从3个选测项目中任选两项进行测试.
(1)小明因游泳测试获得了满分,求他在3个选测项目中选择“一分钟跳绳”项目的概率.
(2)若小红和小慧的游泳测试都未得满分,她们都必须从3个选测项目中选择两项进行体育中考测试,请用列表(或画树状图)的方法,求出小红和小慧选择的两个项目完全相同的概率.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com