
点B.C.E在同一直线上,点A.D在直线CE的同侧,AB=AC,EC=ED,∠BAC=∠CED,直线AE、BD交于点F。
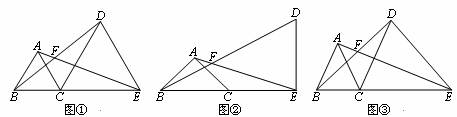
(1)如图①,若∠BAC=60°,则∠AFB=_________;如图②,若∠BAC=90°,则∠AFB=_________;
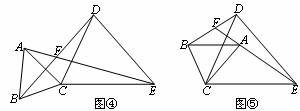
(2)如图③,若∠BAC=α,则∠AFB=_________(用含α的式子表示);
(3)将图③中的△ABC绕点C旋转(点F不与点A.B重合),得图④或图⑤。在图④中,∠AFB与∠α的数量关系是________________;在图⑤中,∠AFB与∠α的数量关系是________________。请你任选其中一个结论证明。
解:


(1)∠AFB=60°,∠AFB=45°.
(2)∠AFB=90°-![]()
![]()
(3)左上图中:∠AFB=90°-![]()
![]() ;右上图中:∠AFB=90°+
;右上图中:∠AFB=90°+![]()
![]() 。
。
∠AFB=90°-![]()
![]() 的证明如下:
的证明如下:
∵AB=AC,EC=ED,∠BAC=∠CED
∴△ABC∽△EDC, ∴![]() ∴∠BCD=∠ACE, ∴△BCD∽△ACE,
∴∠BCD=∠ACE, ∴△BCD∽△ACE,
∴∠CBD=∠CAE.
∠AFB=180°-∠CAE-∠BAC-∠ABD=180°-∠BAC--∠ABC=∠ACB.
∵AB=AC, ∠BAC=![]() ,
,
∴∠ACB=90°-![]()
![]() , ∴∠AFB=90°-
, ∴∠AFB=90°-![]()
![]() .
.
∠AFB=90°+![]()
![]() 的证明如下:
的证明如下:
∵AB=AC,EC=ED,∠BAC=∠CED
∴△ABC∽△EDC, ∴![]() ∴∠BCD=∠ACE, ∴△BCD∽△ACE,
∴∠BCD=∠ACE, ∴△BCD∽△ACE,
∴∠BDC=∠AEC ∴∠AFB=∠BDC+∠CDE+∠DEF=∠CDE+∠CED=180°-∠DCE.
∵AB=AC,EC=ED, ∠BAC=∠DEC=![]() ,
,
∴∠DCE=90°-![]()
![]() , ∴∠AFB=180°-(90°-
, ∴∠AFB=180°-(90°-![]()
![]() )=90°+
)=90°+![]()
![]() .
.


 星级口算天天练系列答案
星级口算天天练系列答案 芒果教辅达标测试卷系列答案
芒果教辅达标测试卷系列答案科目:初中数学 来源:2010年高级中等学校招生全国统一考试数学卷(山东济宁) 题型:选择题
如图(十七),在同一直在线,甲自A点开始追赶等速度前进的乙,且图(十八)长示两人距离与所经时间的线型关系。若乙的速率为每秒1.5公尺,则经过40秒,甲自A点移动多少公尺?
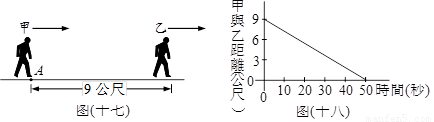
(A) 60 (B) 61.8 (C) 67.2 (D) 69
查看答案和解析>>
科目:初中数学 来源:2010年高级中等学校招生全国统一考试数学卷(四川眉山) 题型:选择题
如图(十七),在同一直在线,甲自A点开始追赶等速度前进的乙,且图(十八)长示两人距离与所经时间的线型关系。若乙的速率为每秒1.5公尺,则经过40秒,甲自A点移动多少公尺?
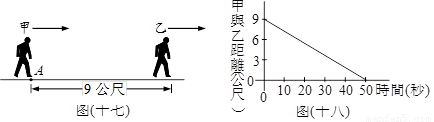
(A) 60 (B) 61.8 (C) 67.2 (D) 69
查看答案和解析>>
科目:初中数学 来源: 题型:
如图1,在同一直在线,甲自A点开始追赶同向前进的乙,且图2长示两人距离与所经时间的线型关系。若乙的速率为每秒 1.5公尺,则经过40秒,甲自A点移动多少公尺?
(A) 60 (B) 61.8 (C) 67.2 (D) 69 。
 |
查看答案和解析>>
科目:初中数学 来源: 题型:
如图(十七),在同一直在线,甲自A点开始追赶等速度前进的乙,且图(十八)长示两人距离与所经时间的线型关系。若乙的速率为每秒1.5公尺,则经过40秒,甲自A点移动多少公尺?

(A) 60 (B) 61.8 (C) 67.2 (D) 69
查看答案和解析>>
科目:初中数学 来源: 题型:

| A.60 | B.61.8 | C.67.2 | D.69 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com