
分析 将原式变形为$\frac{1}{1}$+$\frac{1}{(1+2)×2÷2}$+$\frac{1}{(1+3)×3÷2}$+…+$\frac{1}{(1+2014)×2014÷2}$,进而变形为$\frac{2}{1×2}$+$\frac{2}{2×3}$+$\frac{2}{3×4}$+…+$\frac{2}{2014×2015}$,从而转化为2×(1-$\frac{1}{2015}$)求解.
解答 解:原式=$\frac{1}{1}$+$\frac{1}{(1+2)×2÷2}$+$\frac{1}{(1+3)×3÷2}$+…+$\frac{1}{(1+2014)×2014÷2}$
=$\frac{2}{2}$+$\frac{2}{3×2}$+$\frac{2}{4×3}$+…+$\frac{2}{2015×2014}$
=$\frac{2}{1×2}$+$\frac{2}{2×3}$+$\frac{2}{3×4}$+…+$\frac{2}{2014×2015}$
=2×(1-$\frac{1}{2015}$)
=$\frac{4028}{2015}$.
点评 本题考查了有理数的混合运算的知识,能够正确的变形是解答本题的关键,难度中等.


 激活思维优加课堂系列答案
激活思维优加课堂系列答案 活力试卷系列答案
活力试卷系列答案科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 甲车从A地出发,途径C地时休息一小时,然后按原速度继续前进到达B地;乙车从C地出发到B地后又按原速返回C地,两车同时出发,并以各自的速度匀速行驶,设A,C,B在同一条直线上,如图是甲、乙两车和B地的距离y(千米)与甲车出发时间x(小时)的函数图象.
甲车从A地出发,途径C地时休息一小时,然后按原速度继续前进到达B地;乙车从C地出发到B地后又按原速返回C地,两车同时出发,并以各自的速度匀速行驶,设A,C,B在同一条直线上,如图是甲、乙两车和B地的距离y(千米)与甲车出发时间x(小时)的函数图象.查看答案和解析>>
科目:初中数学 来源: 题型:解答题

查看答案和解析>>
科目:初中数学 来源: 题型:填空题
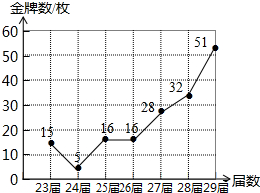 从1984年起,我国先后参加了第23届夏季奥运会,取得了骄人的成绩.如图是根据第23届至29届夏季奥运会我国获得的金牌数绘制的折线统计图,观察统计图可得:与上一届相比增长量最大的是第29届夏季奥运会,比它的上一届增加了19枚金牌.
从1984年起,我国先后参加了第23届夏季奥运会,取得了骄人的成绩.如图是根据第23届至29届夏季奥运会我国获得的金牌数绘制的折线统计图,观察统计图可得:与上一届相比增长量最大的是第29届夏季奥运会,比它的上一届增加了19枚金牌.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
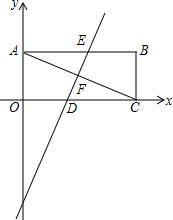 如图,平面直角坐标系中,矩形OABC的两条邻边分别在x轴、y轴上,对角线AC=4$\sqrt{5}$,边OA=4.
如图,平面直角坐标系中,矩形OABC的两条邻边分别在x轴、y轴上,对角线AC=4$\sqrt{5}$,边OA=4.查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com