
【题目】如图,下列条件中,不能证明△ABD≌△ACD的是( )

A. BD=DC ,AB=AC B. ∠ADB=∠ADC,∠BAD=∠CAD
C. ∠B=∠C, BD=DC D. ∠B=∠C ,∠BAD=∠CAD
 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:
【题目】如图,在等边三角形ABC的外侧作直线AP,点C关于直线AP的对称点为点D,连接AD,BD,其中BD交直线AP于点E.
(1)依题意补全图形;(2)若∠PAC=20°,求∠AEB的度数;
(3)连结CE,写出AE, BE, CE之间的数量关系,并证明你的结论.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某高速铁路工程指挥部,要对某路段工程进行招标,接到了甲、乙两个工程队的投标书.从投标书中得知:甲队单独完成这项工程所需天数是乙队单独完成这项工程所需天数的![]() :若由甲队先做20天,剩下的工程再由甲、乙两队合作60天完成.
:若由甲队先做20天,剩下的工程再由甲、乙两队合作60天完成.
(1)求甲、乙两队单独完成这项工程各需多少天?
(2)已知甲队每天的施工费用为8.6万元,乙队每天的施工费用为5.4万元,工程预算的施工费用为1000万元.若在甲、乙工程队工作效率不变的情况下使施工时间最短,问拟安排预算的施工费用是否够用?若不够用,需追加预算多少万元?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】一个多边形的所有内角与它的一个外角之和是2018°,求这个外角的度数和它的边数.
【答案】38° ; 边数13
【解析】试题分析:根据多边形的内角和公式(n-2)180°可知,多边形的内角和是180°的倍数,然后列式求解即可.
试题解析:设多边形的边数是n,加的外角为α,则
(n-2)180°+α=2018°,
α=2378°-180°n,又0<α<180°,
即0<2378°-180°n<180°,
解得: ![]() <n<
<n<![]() ,
,
又n为正整数,
可得n=13,
此时α=38°满足条件,
答:这个外角的度数是38°,它的13边形.
【点睛】本题考查了多边形的内角和公式,利用好多边形的内角和是180°的倍数是解题的关键.
【题型】解答题
【结束】
22
【题目】已知![]() , 求 (1)
, 求 (1) ![]() ; (2)
; (2) ![]() .
.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】(1)填空21-20=2( ); 22-21=2( ) ;23 -22=2( )
(2)请用字母表示第n个等式,并验证你的发现.
(3)利用(2)中你的发现,求20+21+22+23+…+22016+22017的值.
【答案】(1)0,1,2;(2)证明见解析;(3)![]()
【解析】试题分析:(1)根据0次幂的意义和乘方的意义进行计算即可;
(2)观察各等式得到2的相邻两个非负整数幂的差等于其中较小的2的非负整数幂,即2n-2n-1=2n-1(n为正整数);
(3)由于21-20=20,22-21=21,23-22=22,…22018-22017=22017,然后把等式左边与左边相加,右边与右边相加即可求解.
试题解析:(1)21-20=1=20;22-21=2=21;23-22=4=22,
故答案为:0,1,2;
(2)观察可得:2n-2n-1=2n-1(n为正整数),证明如下:
2n-2n-1=2×2n-1-2n-1=2n-1×(2-1)=2n-1;
(3)∵21-20=20,
22-21=21,
23-22=22,
…
22018-22017=22017,
∴22018-20=20+21+22+23+…+22016+22017,
∴20+21+22+23+…+22016+22017的值为22018-1.
【题型】解答题
【结束】
27
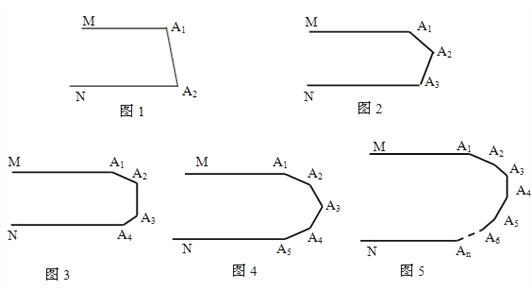
【题目】(1) 如图1,MA1∥NA2,则∠A1+∠A2=_________度.
如图2,MA1∥NA3,则∠A1+∠A2+∠A3=_________ 度.
如图3,MA1∥NA4,则∠A1+∠A2+∠A3+∠A4=_________度.
如图4,MA1∥NA5,则∠A1+∠A2+∠A3+∠A4+∠A5=_________度.
如图5,MA1∥NAn,则∠A1+∠A2+∠A3+…+∠An=_________ 度.
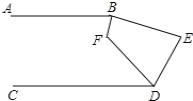
(2) 如图,已知AB∥CD,∠ABE和∠CDE的平分线相交于F,∠E=80°,求∠BFD的度数.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com