
分析 当m,n为有理数时,由求根公式可知,方程x2+mx+n=0的一个根-2+$\sqrt{5}$,则另一根为-2-$\sqrt{5}$,根据两根关系可求m,n的值.
解答 解:由m,n是有理数,且方程x2+mx+n=0有一个根-2+$\sqrt{5}$,是一个无理数;
可知另一根必是已知根的有理化因式即-2-$\sqrt{5}$.
由根与系数的关系,得
$\left\{\begin{array}{l}{(\sqrt{5}-2)+(\sqrt{5}+2)=-m}\\{(\sqrt{5}-2)(\sqrt{5}+2)=n}\end{array}\right.$,
解得$\left\{\begin{array}{l}{m=4}\\{n=-1}\end{array}\right.$.
故答案是:4;-1.
点评 本题主要考查根与系数的关系及系数为有理数时,无理根“成对”出现的原则:x1=a+$\sqrt{b}$,x2=a-$\sqrt{b}$.


 星级口算天天练系列答案
星级口算天天练系列答案 芒果教辅达标测试卷系列答案
芒果教辅达标测试卷系列答案科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 张伟家与一条东西走向的公路之间有一池塘,在学习了“锐角三角函数”一章后,为测量他家到公路之间的距离,张伟在公路上选取了两点B、C,测得他家分别在B处的北偏东30°,C处的西北方向上,且BC=200米,请你计算张伟家到公路的距离.
张伟家与一条东西走向的公路之间有一池塘,在学习了“锐角三角函数”一章后,为测量他家到公路之间的距离,张伟在公路上选取了两点B、C,测得他家分别在B处的北偏东30°,C处的西北方向上,且BC=200米,请你计算张伟家到公路的距离.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
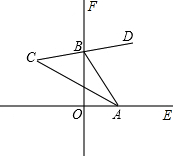 如图,小明想出了一个不利用量角器只利用尺规作图作一个特殊角的方法,他首先作两条互相垂直的直线OE、OF,点A和点B分别是射线OE、OF上任意一点;然后作∠ABF的平分线BD,BD的反向延长线交∠OAB的平分线于点C,则∠C就是所要求作的角,你知道小明作出的∠C是多少度吗?并说明理由.
如图,小明想出了一个不利用量角器只利用尺规作图作一个特殊角的方法,他首先作两条互相垂直的直线OE、OF,点A和点B分别是射线OE、OF上任意一点;然后作∠ABF的平分线BD,BD的反向延长线交∠OAB的平分线于点C,则∠C就是所要求作的角,你知道小明作出的∠C是多少度吗?并说明理由.查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 1 | B. | 2 | C. | 3 | D. | 4 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com