
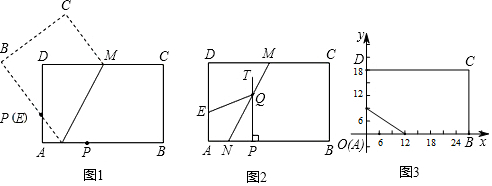
分析 (1)如图2中,连接EP.首先求出EP,根据等腰直角三角形的性质,可知△PFQ1是等腰直角三角形,求出PQ1即可.
(2)首先求出PE,再证明△APE∽△FQ2P,得$\frac{PE}{P{Q}_{2}}$=$\frac{AE}{PF}$,由此即可求出PQ2解决问题.
(3)这些点形成的图象是一段抛物线.利用待定系数法可得函数关系式:y=$\frac{1}{12}$x2+3(0≤x≤26).
解答 解:(1)如图2中,连接EP.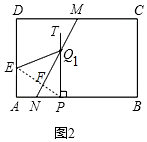
在Rt△APE中,AE=6.AP=6,∠EAP=90°
∴EP=$\sqrt{{6}^{2}+{6}^{2}}$=6$\sqrt{2}$,
∴EF=PF=3$\sqrt{2}$,∠APE=∠FPQ1=45°,
∴PF=FQ1=3$\sqrt{2}$,
∴PQ1=$\sqrt{2}$PF=6,
∴Q1(6,6).
故答案为(6,6).
(2)如图3中,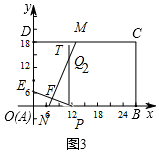
∵∠APE+∠Q2PF=90°,∠Q2PF+∠PQ2F=90°,
∴∠APE=∠PQ2F,∵∠A=∠PFQ2=90°,
∴△APE∽△FQ2P,
∴$\frac{PE}{P{Q}_{2}}$=$\frac{AE}{PF}$,
∴$\frac{6\sqrt{5}}{P{Q}_{2}}$=$\frac{6}{3\sqrt{5}}$,
∴PQ2=15,
∴Q2(12,15).
(3)这些点形成的图象是一段抛物线.
设抛物线的解析式为y=ax2+bx+c,把(0,3),(6,6),(12,15)代入解析式得到
$\left\{\begin{array}{l}{c=3}\\{36a+6b+c=6}\\{144a+12b+c=15}\end{array}\right.$,解得$\left\{\begin{array}{l}{a=\frac{1}{12}}\\{b=0}\\{c=3}\end{array}\right.$,
函数关系式:y=$\frac{1}{12}$x2+3(0≤x≤26).
点评 本题考查四边形综合题、相似三角形的判定和性质、等腰直角三角形的判定和性质、勾股定理、二次函数等知识,解题的关键是正确寻找相似三角形解决问题,学会构建二次函数解决实际问题,属于中考压轴题.


 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:填空题
 如图,已知A,E,F,C在同一条直线上,∠A=∠C,AE=CF,要使△ADF≌△CBE,还需要添加一个条件,这个条件可以是AD=BC(只需写出一个)
如图,已知A,E,F,C在同一条直线上,∠A=∠C,AE=CF,要使△ADF≌△CBE,还需要添加一个条件,这个条件可以是AD=BC(只需写出一个)查看答案和解析>>
科目:初中数学 来源: 题型:填空题
 如图,在△ABC中,AB=AC,AF是BC边上的高,点E、D是AF的三等分点,若△ABC的面积为12cm2,则图中全部阴影部分的面积是6cm2.
如图,在△ABC中,AB=AC,AF是BC边上的高,点E、D是AF的三等分点,若△ABC的面积为12cm2,则图中全部阴影部分的面积是6cm2.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com