
【题目】(问题情境)如图![]() ,
,![]() 中,
中,![]() ,
,![]() ,我们可以利用
,我们可以利用![]() 与
与![]() 相似证明
相似证明![]() ,这个结论我们称之为射影定理,试证明这个定理;
,这个结论我们称之为射影定理,试证明这个定理;
(结论运用)如图![]() ,正方形
,正方形![]() 的边长为
的边长为![]() ,点
,点![]() 是对角线
是对角线![]() 、
、![]() 的交点,点
的交点,点![]() 在
在![]() 上,过点
上,过点![]() 作
作![]() ,垂足为
,垂足为![]() ,连接
,连接![]() ,
,
(1)试利用射影定理证明![]() ;
;
(2)若![]() ,求
,求![]() 的长.
的长.
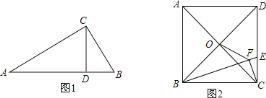
【答案】【问题情境】证明见解析;【结论运用】![]() 证明见解析;(2)
证明见解析;(2)![]() .
.
【解析】
通过证明Rt△ACD∽Rt△ABC得到AC:AB=AD:AC,然后利用比例性质即可得到AC2=ADAB;
【结论运用】
(1)根据射影定理得BC2=BOBD,BC2=BFBE,则BOBD=BFBE,即![]() =
=![]() ,加上∠OBF=∠EBD,于是可根据相似三角形的判定得到△BOF∽△BED;
,加上∠OBF=∠EBD,于是可根据相似三角形的判定得到△BOF∽△BED;
(2)先计算出DE=4,CE=2,BE=2![]() ,OB=3
,OB=3![]() ,再利用(1)中结论△BOF∽△BED得到
,再利用(1)中结论△BOF∽△BED得到![]() =
=![]() ,即
,即![]() =
=![]() ,然后利用比例性质求OF.
,然后利用比例性质求OF.
如图1.
∵CD⊥AB,∴∠ADC=90°,而∠CAD=∠BAC,∴Rt△ACD∽Rt△ABC,∴AC:AB=AD:AC,∴AC2=ADAB;
(1)如图2.
∵四边形ABCD为正方形,∴OC⊥BO,∠BCD=90°,∴BC2=BOBD.
∵CF⊥BE,∴BC2=BFBE,∴BOBD=BFBE,即![]() =
=![]() ,而∠OBF=∠EBD,∴△BOF∽△BED;
,而∠OBF=∠EBD,∴△BOF∽△BED;
(2)∵BC=CD=6,而DE=CE,∴DE=4,CE=2.
在Rt△BCE中,BE=![]() =2
=2![]() .在Rt△OBC中,OB=
.在Rt△OBC中,OB=![]() BC=3
BC=3![]() .
.
∵△BOF∽△BED,∴![]() =
=![]() ,即
,即![]() =
=![]() ,∴OF=
,∴OF=![]() .
.


 名师导航单元期末冲刺100分系列答案
名师导航单元期末冲刺100分系列答案 名校名卷单元同步训练测试题系列答案
名校名卷单元同步训练测试题系列答案科目:初中数学 来源: 题型:
【题目】二次函数![]() ,
,![]() ,
,![]() 是常数,且
是常数,且![]() 中的
中的![]() 与
与![]() 的部分对应值如下表所示,则下列结论中,正确的个数有( )
的部分对应值如下表所示,则下列结论中,正确的个数有( )
|
|
|
|
|
|
|
|
|
|
![]() ;
;![]() 当
当![]() 时,
时,![]() ;
;![]() 当
当![]() 时,
时,![]() 的值随
的值随![]() 值的增大而减小;
值的增大而减小;
![]() 方程
方程![]() 有两个不相等的实数根.
有两个不相等的实数根.
A. 4个 B. 3个 C. 2个 D. 1个
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】小王的学校举行了一次年级考试,考了若干门课程,后加试了一门,小王考得![]() 分,这时小王的平均成绩比最初的平均成绩提高了
分,这时小王的平均成绩比最初的平均成绩提高了![]() 分.后来又加试了一门,小王考得
分.后来又加试了一门,小王考得![]() 分,这时小王的平均成绩比最初的平均成绩下降了
分,这时小王的平均成绩比最初的平均成绩下降了![]() 分,则小王共考了(含加试的两门)________门课程,最后平均成绩为________分.
分,则小王共考了(含加试的两门)________门课程,最后平均成绩为________分.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,有长为24m的篱笆,围成中间隔有一道篱笆的长方形的花圃,且花圃的长可借用一段墙体(墙体的最大可用长度a=10m).
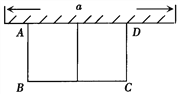
(1)如果所围成的花圃的面积为45m2,试求宽AB的长;
(2)按题目的设计要求,能围成面积比45m2更大的花圃吗?如果能,请求出最大面积,并说明围法;如果不能,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
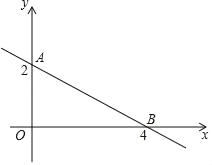
【题目】如图,直线AB与x轴,y轴的交点为A,B两点,点A,B的纵坐标、横坐标如图所示.
(1)求直线AB的表达式及△AOB的面积S△AOB.
(2)在x轴上是否存在一点,使S△PAB=3?若存在,求出P点的坐标,若不存在,说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图1,在![]() 中,
中,![]() ,
,![]() ,
,![]() 于点
于点![]() ,
,![]() ,点
,点![]() 在
在![]() 上,射线
上,射线![]() ,
,![]() 分别交
分别交![]() ,
,![]() 两边于
两边于![]() ,
,![]() 两点
两点
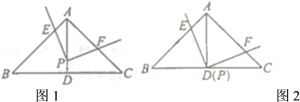
(1)当点![]() 与点
与点![]() 重合时,如图11—2所示,直接写出:
重合时,如图11—2所示,直接写出:
①![]() 与
与![]() 之间的数量关系:_____________________;
之间的数量关系:_____________________;
②![]() 与
与![]() 之间的数量关系:_______________________;
之间的数量关系:_______________________;
(2)当点![]() 在线段
在线段![]() 上时(不与端点重合,如图2所示,则(1)中②的结论还成立吗?若成立,请证明这个结论;若不成立,请举反例说明
上时(不与端点重合,如图2所示,则(1)中②的结论还成立吗?若成立,请证明这个结论;若不成立,请举反例说明
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在半径为![]() 的扇形
的扇形![]() 中,
中,![]() ,点
,点![]() 是弧
是弧![]() 上的一个动点(不与点
上的一个动点(不与点![]() 、
、![]() 重合)
重合)![]() ,
,![]() ,垂足分别为
,垂足分别为![]() 、
、![]() .
.

![]() 当
当![]() 时,求线段
时,求线段![]() 的长;
的长;
![]() 在
在![]() 中是否存在长度保持不变的边?如果存在,请指出并求其长度,如果不存在,请说明理由;
中是否存在长度保持不变的边?如果存在,请指出并求其长度,如果不存在,请说明理由;
![]() 设
设![]() ,
,![]() 的面积为
的面积为![]() ,求
,求![]() 关于
关于![]() 的函数关系式,并写出
的函数关系式,并写出![]() 的范围.
的范围.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】小明在学习过程中,对教材中的一个有趣问题做如下探究:

(习题回顾)已知:如图1,在![]() 中,
中,![]() ,
,![]() 是角平分线,
是角平分线,![]() 是高,
是高,![]() 、
、![]() 相交于点
相交于点![]() .求证:
.求证:![]() ;
;
(变式思考)如图2,在![]() 中,
中,![]() ,
,![]() 是
是![]() 边上的高,若
边上的高,若![]() 的外角
的外角![]() 的平分线交
的平分线交![]() 的延长线于点
的延长线于点![]() ,其反向延长线与
,其反向延长线与![]() 边的延长线交于点
边的延长线交于点![]() ,则
,则![]() 与
与![]() 还相等吗?说明理由;
还相等吗?说明理由;
(探究延伸)如图3,在![]() 中,
中,![]() 上存在一点
上存在一点![]() ,使得
,使得![]() ,
,![]() 的平分线
的平分线![]() 交
交![]() 于点
于点![]() .
.![]() 的外角
的外角![]() 的平分线所在直线
的平分线所在直线![]() 与
与![]() 的延长线交于点
的延长线交于点![]() .直接写出
.直接写出![]() 与
与![]() 的数量关系.
的数量关系.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com