
【题目】七巧板是我国祖先的一项卓越创造,如图正方形ABCD可以制作一副七巧板,现将这副七巧板拼成如图2的“风车”造型(内部有一块空心),连结最外围的风车顶点M、N、P、Q得到一个四边形MNPQ,则正方形ABCD与四边形MNPQ的面积之比为( )
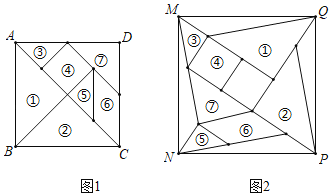
A.5:8B.3:5C.8:13D.25:49
科目:初中数学 来源: 题型:
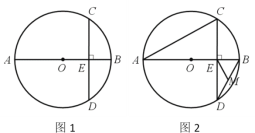
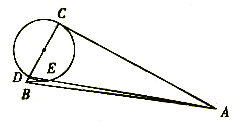
【题目】已知AB是⊙O的直径,C是⊙O上的一点(不与点A,B重合),过点C作AB的垂线交⊙O于点D,垂足为E点.
(1)如图1,当AE=4,BE=2时,求CD的长度;
(2)如图2,连接AC,BD,点M为BD的中点.求证:ME⊥AC.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在△ABC中,AB=AC=5,BC=4![]() ,D为边AB上一动点(B点除外),以CD为一边作正方形CDEF,连接BE,则△BDE面积的最大值为______.
,D为边AB上一动点(B点除外),以CD为一边作正方形CDEF,连接BE,则△BDE面积的最大值为______.

查看答案和解析>>
科目:初中数学 来源: 题型:
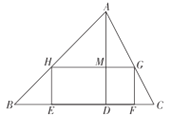
【题目】如图所示,要在底边BC=160cm,高AD=120cm的△ABC铁皮余料上,截取一个矩形EFGH,使点H在AB上,点G在AC上,点E,F在BC上,AD交HG于点M.
(1)设矩形EFGH的长HG=ycm,宽HE=xcm.求y与x的函数关系式;
(2)当x为何值时,矩形EFGH的面积S最大?最大值是多少?
查看答案和解析>>
科目:初中数学 来源: 题型:
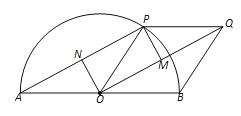
【题目】如图,已知AB为半圆O的直径,P为半圆上的一个动点(不含端点),以OP、OB为一组邻边作POBQ,连接OQ、AP,设OQ、AP的中点分别为M、N,连接PM、ON.
(1)试判断四边形OMPN的形状,并说明理由.
(2)若点P从点B出发,以每秒15°的速度,绕点O在半圆上逆时针方向运动,设运动时间为ts.
①试求:当t为何值时,四边形OMPN的面积取得最大值?并判断此时直线PQ与半圆O的位置关系(需说明理由);
②是否存在这样的t,使得点Q落在半圆O内?若存在,请直接写出t的取值范围;若不存在,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】学校为奖励在家自主学习有突出表现的学生,决定购买笔记本和钢笔作为奖品.已知1本笔记本和4支钢笔共需100元,4本笔记本和6支钢笔共需190元.
(1)分别求一本笔记本和一支钢笔的售价;
(2)若学校准备购进这两种奖品共90份,并且笔记本的数量不多于钢笔数量的3倍,请设计出最省钱的购买方案,并说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在Rt△ABC中,∠ACB=90°.AC=8,BC=3,点D是BC边上动点,连接AD交以CD为直径的圆于点E,则线段BE长度的最小值为( )
A.1B.![]() C.
C. ![]() D.
D.![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】“某市为处理污水,需要铺设一条长为4000米的管道,为了尽量减少施工对交通所造成的影响,实际施工时×××××.设原计划每天铺设管道x米,则可得方程![]() .”根据此情境,题中用“×××××”表示得缺失的条件,应补为( )
.”根据此情境,题中用“×××××”表示得缺失的条件,应补为( )
A.每天比原计划多铺设10米,结果延期20天才完成任务
B.每天比原计划少铺设10米,结果延期20天才完成任务
C.每天比原计划多铺设10米,结果提前20天完成任务
D.每天比原计划少铺设10米,结果提前20天完成任务
查看答案和解析>>
科目:初中数学 来源: 题型:
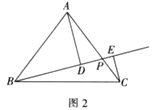
【题目】问题提出
(1)如图1,已知三角形![]() ,请在
,请在![]() 边上确定一点
边上确定一点![]() ,使得
,使得![]() 的值最小.
的值最小.
问题探究
(2)如图2,在等腰![]() 中,
中,![]() ,点
,点![]() 是
是![]() 边上一动点,分别过点
边上一动点,分别过点![]() ,点
,点![]() 作线段
作线段![]() 所在直线的垂线,垂足为点
所在直线的垂线,垂足为点![]() ,若
,若![]() ,求线段
,求线段![]() 的取值范围,并求
的取值范围,并求![]() 的最大值.
的最大值.
问题解决
(3)如图3,正方形![]() 是一块蔬菜种植基地,边长为3千米,四个顶点处都建有一个蔬菜采购点,根据运输需要,经过顶点
是一块蔬菜种植基地,边长为3千米,四个顶点处都建有一个蔬菜采购点,根据运输需要,经过顶点![]() 处和
处和![]() 边的两个三等分点
边的两个三等分点![]() 之间的某点
之间的某点![]() 建设一条向外运输的快速通道,其余三个采购点都修建垂直于快速通道的蔬菜输送轨道,分别为
建设一条向外运输的快速通道,其余三个采购点都修建垂直于快速通道的蔬菜输送轨道,分别为![]() 、
、![]() 、
、![]() .若你是此次项目设计的负责人,要使三条运输轨道的距离之和
.若你是此次项目设计的负责人,要使三条运输轨道的距离之和![]() 最小,你能不能按照要求进行规划,请通过计算说明.
最小,你能不能按照要求进行规划,请通过计算说明.

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com