
如图,y=-x+3交x轴于点A,交y轴于点B,抛物线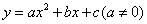 经过A,B,C(1,0)三点.
经过A,B,C(1,0)三点.
(1)求抛物线解析式.
(2)若点D的坐标为(-1,0),在直线y=-x+3上有一点P使△ABO与△ADP相似,求出点P的坐标.
(3)在(2)的条件下,且点P为第一象限内的点,过点P作PM⊥y轴于点M,过点A作直线l平行于y轴,动点N从原点出发以每秒一个单位的速度沿0-M-P运动,同时直线l从A点出发以相同的速度沿x轴向左平移,在平移过程中,直线l交x轴于点R,交线段BP或OP于点Q,当点M达到P点时运动停止,在运动过程中,设动点N的运动时间为t秒,是否存在以P,Q,N为顶点的三角形是等腰三角形?若存在,求出t的值;若不存在请说明理由.
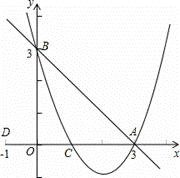
(1)由题意得,A(3,0),B(0,3)
∵抛物线经过A、B、C三点,
∴把A(3,0),B(0,3),C(1,0)三点分别代入y=ax2+bx+c,
解得y=x2-4x+3. ……………(2分)
(2)由题意可得,△ABO为等腰三角形,
①若△ABO∽△APD,则 ,
,
 DP=AD=4.
DP=AD=4.
 P(-1,4)……………(1分)
P(-1,4)……………(1分)
②若△ABO∽△ADP,过点P作PE⊥x轴于E,AD=4
 △ABO为等腰三角形
△ABO为等腰三角形
 △ADP是等腰三角形,
△ADP是等腰三角形,
由“等腰三角形三线合一”可得,DE=AE=2=PE,即点E与点C重合,
 P(1,2) ……………(1分)
P(1,2) ……………(1分)
(3)当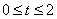 时,可得PN=PQ,t=1. ……………(2分)
时,可得PN=PQ,t=1. ……………(2分)
当2< 时,①可得QN=QP,t=
时,①可得QN=QP,t=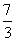 .……………(2分)
.……………(2分)
②可得QN=PQ,t=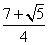 .……………(2分)
.……………(2分)
③可得QN=NP,t= .
.


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:初中数学 来源: 题型:
某生产“科学计算器”的公司, 有100名职工,该公司生产的计算器由百货公司代理销售,经公司多方考察,发现公司的生产能力受到限制.决定引进一条新的计算器生产线生产计算器,并从这100名职工中选派一部分人到新生产线工作.分工后,继续在原生产线从事计算器生产的职工人均年产值可增加20%,而分派到新生产线的职工人均年产值为分工前人均年产值的4倍,如果要保证公司分工后,原生产线生产计算器的年总产值不少于分工前公司生产计算器的年总产值,而新生产线生产计算器的年总产值不少于分工前公司生产计算器的年总产值的一半.
(1)试确定分派到新生产线的人数;
(2)当多少人参加新生产线生产时,公司年总产值最大?相比分工前,公司年总产值的增长率是多少?
查看答案和解析>>
科目:初中数学 来源: 题型:
设二次函数y=ax2+bx+c(a>0)的图象与x轴的两个交点A(x1,0),B(x2,0),抛物线的顶点为C,显然△ABC为等腰三角形.
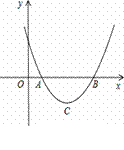 (1)当△ABC为等腰直角三角形时,求
(1)当△ABC为等腰直角三角形时,求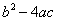 的值;
的值;
(2)当△ABC为等边三角形时,求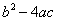 的值.
的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
游泳池里,一些小朋友正在老师的指导下练习游泳,男孩们带的都是天蓝色泳帽,女孩们带的都是粉红色泳帽。在每一个男孩看来,天蓝色的游泳帽与粉红色的游泳帽一样多;而在每一个女孩看来,天蓝色的游泳帽比粉红色游泳帽多一倍。则男孩有 人。
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com