

分析 (1)作A点关于MN的对称点A′,连接PA′、PA、PB,则PA+PB=PA′+PB,根据两点之间线段最短,可得线段BA′与MN的交点P即为所求点;
(2)要使P得到A、B的距离相等,点P应在线段AB的垂直平分线上;要使P到两条公路的距离相等,点P应在两条公路所在直线夹角的平分线上,因而线段AB的垂直平分线与两条公路所在直线夹角的平分线的交点P、P′即为所求点.
解答 解:(1)作A点关于MN的对称点A′,连接BA′交MN与点P,如图1,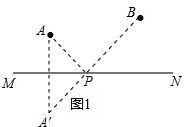
P为所求点;
(2)作线段AB的垂直平分线,作直线CD与直线MN夹角平分线,如图2,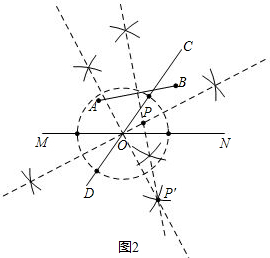
线段AB的垂直平分线与两条公路所在直线夹角的平分线的交点P、P′即为所求点.
点评 本题是一道作图题,主要考查了线段垂直平分线的性质及角平分线的性质等知识,需要注意的是两条直线所成的角有四个,这四个角的角平分线上的点到这两条直线的距离都相等.


 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
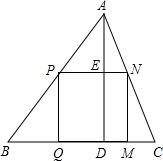 如图,△ABC为一锐角三角形,BC=12,BC边上的高AD=8.点Q,M在边BC上,P,N分别在边AB,AC上,且PNMQ为矩形.
如图,△ABC为一锐角三角形,BC=12,BC边上的高AD=8.点Q,M在边BC上,P,N分别在边AB,AC上,且PNMQ为矩形.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
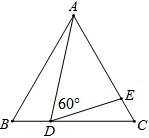 已知:如图,△ABC是等边三角形,点D、E分别在边BC、AC上,∠ADE=60°.
已知:如图,△ABC是等边三角形,点D、E分别在边BC、AC上,∠ADE=60°.查看答案和解析>>
科目:初中数学 来源: 题型:选择题
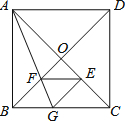 如图,在正方形ABCD中,AC、BD相交于点O,把△ABC折叠,使AB落在AC上,点B与AC上的点E重合,展开后,折痕AG交BD于点F,连结EG、EF.下列结论:
如图,在正方形ABCD中,AC、BD相交于点O,把△ABC折叠,使AB落在AC上,点B与AC上的点E重合,展开后,折痕AG交BD于点F,连结EG、EF.下列结论:| A. | 1个 | B. | 2个 | C. | 3个 | D. | 4个 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
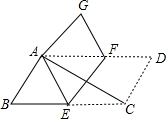 如图,将平行四边形ABCD纸片沿EF折叠,使点C与点A重合,点D落在点G处,
如图,将平行四边形ABCD纸片沿EF折叠,使点C与点A重合,点D落在点G处,查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com