练习册

  • 练习册
  • 试题
    精英家教网 > 初中数学 > 题目详情
    3．下列说法中正确的是（　　）
    A．“任意画出一个等边三角形，它是轴对称图形”是随机事件
    B．“概率为0.001的事件”是不可能事件
    C．“任意画出一个平行四边形，它是中心对称图形”是必然事件
    D．任意掷一枚质地均匀的硬币10次，正面向上的一定是5次

    分析 首先利用随机事件以及必然事件的定义对各选项进行判断得出答案．

    解答 解：A、任意画出一个等边三角形，它是轴对称图形”是必然事件，故此选项错误；
    B、“概率为0.001的事件”是随机事件，故此选项错误；
    C、任意画出一个平行四边形，它是中心对称图形”是必然事件，正确；
    D、任意掷一枚质地均匀的硬币10次，正面向上的不一定是5次，故此选项错误．
    故选：C．

    点评 此题主要考查了随机事件，正确把握相关事件的定义是解题关键．

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：初中数学 来源： 题型：选择题

    6．下列统计量中，反映一组数据波动情况的是（　　）
    A．平均数B．众数C．频率D．方差

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

    14．小王同学准备筹集资金为贫困山区儿童捐款，打算从淘宝网上购进一批闪光发箍和荧光棒在某演唱会现场出售，其中闪光发箍的购买价格为6元/个，荧光棒的购买价格为8元/个．
    （1）小王计划购进闪光发箍和荧光棒共120个，且将闪光发箍加价40%、荧光棒加价20%后出售．当所有物品售完后，若利润不低于256元，则小王至少应购买闪光发箍多少个？
    （2）小王调整了方案，决定将闪光发箍的售价在进价的基础上上涨（a+10）%、荧光棒的售价在进价基础上上涨a%，在（1）中闪光发箍购买量取得最小值的情况下，将闪光发箍的购买量提高$\frac{5}{3}$a%，而荧光棒的购买量保持不变，则全部售出后，最终可获利384元，请求出a的值．

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

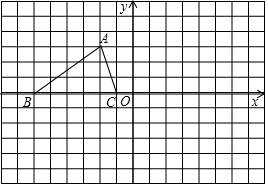    11．如图，在边长为1个单位长度的小正方形组成的网格中，给出了格点△ABC（顶点是网格线的交点），已知△ABC三个顶点的坐标分别为A（-2，3）、B（-6，0）、C（-1，0）
    （1）经过怎样的平移，可使△ABC的顶点A与坐标原点O重合，画出平移后的三角形△OB′C′．
    （2）已知△ABC的重心G的坐标为（a，b），请直接写出△OB′C′的重心G′的坐标（分别用a、b的代数式表示）；
    （3）将△ABC绕坐标原点O逆时针旋转90°，得到△A′'B′'C′'，画出△A′'B′'C′'．

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

    18．如图1，已知△ABC的三顶点坐标分别为A（-1，-1），B（3，-1），C（0，-4），二次函数y=ax2+bx+c恰好经过A、B、C三点．
    （1）求二次函数的解析式；
    （2）如图1，若点P是△ABC边AB上的一个动点，过点P作PQ∥AC，交BC于点Q，连接CP，当△CPQ的面积最大时，求点P的坐标；
    （3）如图2，点M是直线y=x上的一个动点，点N是二次函数图象上的一动点，若△CMN构成以CN为斜边的等腰直角三角形，直接写出所有满足条件的点N的横坐标．

    查看答案和解析>>

    科目：初中数学 来源： 题型：填空题

    8．在单词mathcmatics（数学）中任意选择一个字母，字母为“m”的概率为$\frac{2}{11}$．

    查看答案和解析>>

    科目：初中数学 来源： 题型：选择题

    15．下列计算正确的是（　　）
    A．a3+a2=2a5B．a3•a2=a6C．a3÷a2=aD．（a3）2=a9

    查看答案和解析>>

    科目：初中数学 来源： 题型：选择题

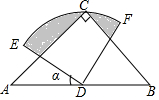    12．如图，在△ABC中，CA=CB，∠ACB=90°，以AB的中点D为圆心，作圆心角为90°的扇形DEF，点C恰在EF上，设∠ADE=α（0°＜α＜90°），当α由小到大变化时，图中阴影部分的面积（　　）
    A．由小变大B．由大变小
    C．不变D．先由小变大，后由大变小

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

    13．问题呈现：
    如图1，点E、F、G、H分别在矩形ABCD的边AB、BC、CD、DA上，AE=DG，求证：2S四边形EFGH=S矩形ABCD．（S表示面积）
    实验探究：
    某数学实验小组发现：若图1中AH≠BF，点G在CD上移动时，上述结论会发生变化，分别过点E、G作BC边的平行线，再分别过点F、H作AB边的平行线，四条平行线分别相交于点A1、B1、C1、D1，得到矩形A1B1C1D1．
    如图2，当AH＞BF时，若将点G向点C靠近（DG＞AE），经过探索，发现：2S四边形EFGH=S矩形ABCD+S${\;}_{矩形{A}_{1}{B}_{1}{C}_{1}{D}_{1}}$．
    如图3，当AH＞BF时，若将点G向点D靠近（DG＜AE），请探索S四边形EFGH、S矩形ABCD与S${\;}_{矩形{A}_{1}{B}_{1}{C}_{1}{D}_{1}}$之间的数量关系，并说明理由．
    迁移应用：
    请直接应用“实验探究”中发现的结论解答下列问题：
    （1）如图4，点E、F、G、H分别是面积为25的正方形ABCD各边上的点，已知AH＞BF，AE＞DG，S四边形EFGH=11，HF=$\sqrt{29}$，求EG的长．
    （2）如图5，在矩形ABCD中，AB=3，AD=5，点E、H分别在边AB、AD上，BE=1，DH=2，点F、G分别是边BC、CD上的动点，且FG=$\sqrt{10}$，连接EF、HG，请直接写出四边形EFGH面积的最大值．

    查看答案和解析>>

    同步练习册答案