
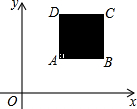
 如图,有一种动画程序,屏幕上正方形ABCD是黑色区域(含边界),其中A(1,1),B(2,1),C(2,2),D(1,2).用信号枪沿直线y=kx(k>0)发射信号.当信号遇到黑色区域时,区域便由黑变白,若没遇到黑色区域,则无变化,无变化的区域即为信号枪使用的盲区,则使信号枪成为盲区的k的取值范围是
如图,有一种动画程序,屏幕上正方形ABCD是黑色区域(含边界),其中A(1,1),B(2,1),C(2,2),D(1,2).用信号枪沿直线y=kx(k>0)发射信号.当信号遇到黑色区域时,区域便由黑变白,若没遇到黑色区域,则无变化,无变化的区域即为信号枪使用的盲区,则使信号枪成为盲区的k的取值范围是科目:初中数学 来源: 题型:
| A、(-4,5) |
| B、(5,-4) |
| C、(7,-4) |
| D、(-4,7) |
查看答案和解析>>
科目:初中数学 来源: 题型:
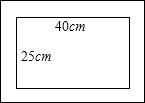 如图,一幅矩形油画的长为40cm,宽为25cm,此幅油画的外围镶有画框.已知画框的宽度为5cm,则画框内外所构成的两个矩形的长和宽成比例吗?说明理由.
如图,一幅矩形油画的长为40cm,宽为25cm,此幅油画的外围镶有画框.已知画框的宽度为5cm,则画框内外所构成的两个矩形的长和宽成比例吗?说明理由.查看答案和解析>>
科目:初中数学 来源: 题型:
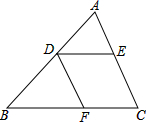 如图,在△ABC中,点D,E,F分别在边AB,AC,BC上,DE∥BC,DF∥AC,已知
如图,在△ABC中,点D,E,F分别在边AB,AC,BC上,DE∥BC,DF∥AC,已知| AD |
| BD |
| 2 |
| 3 |
查看答案和解析>>
科目:初中数学 来源: 题型:
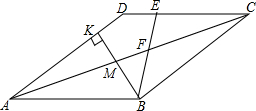 如图,菱形ABCD中,一射线BE分∠ABC为∠ABE与∠CBE,且∠ABE:∠CBE=7:3,BE交对角线AC于F,交CD于E,过B作BK⊥AD于K点,交AC于M,且∠DAC=15°.
如图,菱形ABCD中,一射线BE分∠ABC为∠ABE与∠CBE,且∠ABE:∠CBE=7:3,BE交对角线AC于F,交CD于E,过B作BK⊥AD于K点,交AC于M,且∠DAC=15°.查看答案和解析>>
科目:初中数学 来源: 题型:

| 1 |
| 3 |
| 1 |
| 3 |
| 1 |
| 3 |
| 1 |
| 3 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com