练习册

  • 练习册
  • 试题
    精英家教网 > 初中数学 > 题目详情

    如图，一起重机的机身高21米，吊杆AB长36米，吊杆与水平线的夹角∠BAC可从升到．求起重机起吊的最大高度(吊钩本身的长度和所挂重物的高度忽略不计)和当起重机位置不变时可使用的最大水平距离(精确到0.1米，＝0.9848，＝0.1736，≈1.732)．

    答案：
    解析：

    　　解：在Rt△ABC中，当∠BAC＝时，

    　　BC＝AB·

    　　＝36×0.9848≈35.5(米)．

    　　35.5＋21＝56.5(米)．

    　　当∠BAC＝时，

    　　AC＝AB·＝36×＝18

    　　≈18×1.732≈31.2(米)．

    　　答：最大高度约为56.5米，最大水平距离约31.2米．


    提示：

    　　这是一个解直角三角形的应用问题．当已知直角三角形的边与角时，可利用三角函数，求未知的边．


    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：初中数学 来源： 题型：

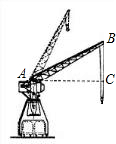    精英家教网如图，一起重机的机身高21m，吊杆AB长36m，吊杆与水平线的夹角∠BAC可从30°升到80°．求起重机起吊的最大高度（吊钩本身的长度和所挂重物的高度忽略不计）和当起重机位置不变时使用的最大水平距离（精确到0.1米，sin80°=0.9848，cos80°=0.1736，
    		3
    ≈1.732）

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

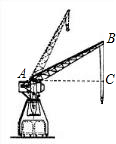    如图，一起重机的机身高21m，吊杆AB长36m，吊杆与水平线的夹角∠BAC可从30°升到80°．求起重机起吊的最大高度（吊钩本身的长度和所挂重物的高度忽略不计）和当起重机位置不变时使用的最大水平距离（精确到0.1米，sin80°=0.9848，cos80°=0.1736，数学公式≈1.732）

    查看答案和解析>>

    科目：初中数学 来源：2000年全国中考数学试题汇编《锐角三角函数》（03）（解析版） 题型：解答题

    （2000•吉林）如图，一起重机的机身高21m，吊杆AB长36m，吊杆与水平线的夹角∠BAC可从30°升到80°．求起重机起吊的最大高度（吊钩本身的长度和所挂重物的高度忽略不计）和当起重机位置不变时使用的最大水平距离（精确到0.1米，sin80°=0.9848，cos80°=0.1736，≈1.732）

    查看答案和解析>>

    科目：初中数学 来源：2000年吉林省中考数学试卷（解析版） 题型：解答题

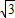    （2000•吉林）如图，一起重机的机身高21m，吊杆AB长36m，吊杆与水平线的夹角∠BAC可从30°升到80°．求起重机起吊的最大高度（吊钩本身的长度和所挂重物的高度忽略不计）和当起重机位置不变时使用的最大水平距离（精确到0.1米，sin80°=0.9848，cos80°=0.1736，≈1.732）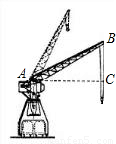

    查看答案和解析>>

    同步练习册答案