
分析 (1)首先计算乘方,然后从左向右依次计算即可.
(2)首先计算乘方,然后计算除法和加法即可.
(3)首先计算除法,然后计算乘法即可.
(4)根据多项式乘多项式的运算方法计算即可.
解答 解:(1)($\frac{2}{3}$)-1+(π-3)0-(-2)-2
=1.5+1-0.25
=2.25
(2)(-2a)3+(a4)2÷(-a)5
=-8a3+a8÷(-a5)
=-8a3-a3
=-9a3
(3)(p-q)4÷(q-p)3•(p-q)5
=-(p-q)•(p-q)5
=-(p-q)6
(4)(2a+b)(2b-a)
=4ab-2a2+2b2-ab
=3ab-2a2+2b2
点评 此题主要考查了整式的混合运算,实数的运算方法,以及零指数幂、负整数指数幂的运算方法,要熟练掌握,解答此题的关键是要明确:有乘方、乘除的混合运算中,要按照先乘方后乘除的顺序运算,其运算顺序和有理数的混合运算顺序相似.


 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:选择题
| A. | 28 | B. | 30 | C. | 45 | D. | 53 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
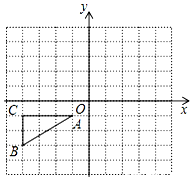 如图,已知△ABC的顶点A,B,C的坐标分别是A(-1,-1),B(-4,-3),C(-4,-1)
如图,已知△ABC的顶点A,B,C的坐标分别是A(-1,-1),B(-4,-3),C(-4,-1)查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
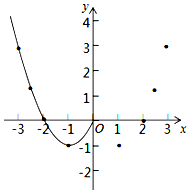 某班“数学兴趣小组”对函数y=x2-2|x|的图象和性质进行了探究,探究过程如下.
某班“数学兴趣小组”对函数y=x2-2|x|的图象和性质进行了探究,探究过程如下.| x | … | -3 | -$\frac{5}{2}$ | -2 | -1 | 0 | 1 | 2 | $\frac{5}{2}$ | 3 | … |
| y | … | 3 | $\frac{5}{4}$ | m | -1 | 0 | -1 | 0 | $\frac{5}{4}$ | 3 | … |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com