
分析 (1)同分母的两个数比较大小,只要比较两个分子的大小即可得出结论;
(2)运用作差的方法进行比较,看所得结果是否大于0即可.
解答 解:(1)∵$\sqrt{3}$<2,
∴$\sqrt{3}$-1<1,
∴$\frac{\sqrt{3}-1}{2}$<$\frac{1}{2}$;
(2)∵($\sqrt{7}$-$\sqrt{2}$)-($\sqrt{5}$-$\sqrt{3}$)=$\sqrt{7}$-$\sqrt{5}$+$\sqrt{3}$-$\sqrt{2}$=($\sqrt{7}$-$\sqrt{5}$)+($\sqrt{3}$-$\sqrt{2}$)>0,
∴$\sqrt{7}$-$\sqrt{2}$>$\sqrt{5}$-$\sqrt{3}$.
点评 本题主要考查了实数大小比较,解题时注意:利用数轴也可以比较任意两个实数的大小,即在数轴上表示的两个实数,右边的总比左边的大,在原点左侧,绝对值大的反而小.


 新非凡教辅冲刺100分系列答案
新非凡教辅冲刺100分系列答案科目:初中数学 来源: 题型:解答题
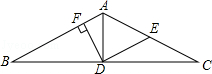 如图,在△ABC中,AB=AC,AD是△ABC的中线,E是AC的中点,连接DE,DF⊥AB于F.求证:
如图,在△ABC中,AB=AC,AD是△ABC的中线,E是AC的中点,连接DE,DF⊥AB于F.求证:查看答案和解析>>
科目:初中数学 来源: 题型:解答题
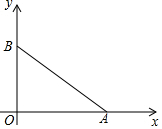 如图,在平面直角坐标系xOy中,已知点(4,0),B(0,3),若有一个直角三角形与Rt△ABO全等且有一条公共的直角边,试写出这个直角三角形未知顶点的坐标.
如图,在平面直角坐标系xOy中,已知点(4,0),B(0,3),若有一个直角三角形与Rt△ABO全等且有一条公共的直角边,试写出这个直角三角形未知顶点的坐标.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com