
| A. | 6048x4011 | B. | 6049x4034 | C. | 6049x4033 | D. | 6048x4035 |
 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:解答题
 李强家里搞装修时,木工师傅想要在一块矩形木板ABCD的中央挖去一个形状与原矩形相同,周长是原矩形一半的小矩形(如图),木工师傅算来算去,不知如何下手,正犯愁时,李强放学回家,见状说:“很方便,连接AC,BD交于点O,用刻度尺分别量出AO,BO,CO,DO的中点E,F,G,H,依次连接EF,FG,GH,HE,就得到要挖去的矩形EFGH.”请你说明道理.
李强家里搞装修时,木工师傅想要在一块矩形木板ABCD的中央挖去一个形状与原矩形相同,周长是原矩形一半的小矩形(如图),木工师傅算来算去,不知如何下手,正犯愁时,李强放学回家,见状说:“很方便,连接AC,BD交于点O,用刻度尺分别量出AO,BO,CO,DO的中点E,F,G,H,依次连接EF,FG,GH,HE,就得到要挖去的矩形EFGH.”请你说明道理.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 在平面直角坐标系中,A、B、C三点的坐标分别为A(-6,7)、B(-3,0)、C(0,3).
在平面直角坐标系中,A、B、C三点的坐标分别为A(-6,7)、B(-3,0)、C(0,3).查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | $\sqrt{2}$+$\sqrt{3}$=$\sqrt{5}$ | B. | 4$\sqrt{3}$-3$\sqrt{3}$=1 | C. | 2$\sqrt{3}$×3$\sqrt{3}$=6$\sqrt{3}$ | D. | $\sqrt{3}$÷$\sqrt{12}$=$\frac{1}{2}$ |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
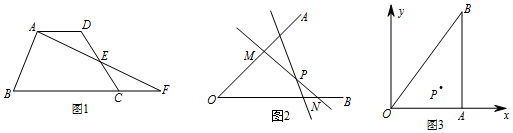
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
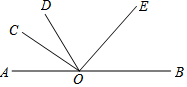 如图,已知点O在直线AB上,∠COE=90°,OD平分∠AOE,∠COD=25°,则∠BOD的度数为( )
如图,已知点O在直线AB上,∠COE=90°,OD平分∠AOE,∠COD=25°,则∠BOD的度数为( )| A. | 100° | B. | 115° | C. | 65° | D. | 130° |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com