
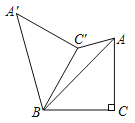
【题目】如图,在Rt△ABC中,∠C=90°,AC=BC=2;若将△ABC绕点B逆时针旋转60°到△A′BC′的位置,连接C′A,则C′A的长为( )
A.![]() B.
B.![]() C.
C.![]() D.2﹣
D.2﹣![]()
【答案】B
【解析】
连接AA′,延长AC′交BA′于点M,证明△AA′M为直角三角形,在Rt△AA′M根据勾股定理可求得AM,在等腰直角三角形A′BC′中根据斜边的中线等于斜边的一半求得MC′,于是AC′可求.
解:如图,连接AA′,延长AC′交BA′于点M,
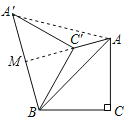
由题意得:∠ABA′=60°,BA=B′A,
∴△BAA′为等边三角形,
∴∠BAA′=60°,AB=A′A;
在△BAC′与△A′AC′中,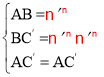 ,
,
∴△BAC′≌△A′AC′(SSS),
∴∠MAA′=∠MAB=30°,
∴AM⊥BA′,且BM=A′M;
由题意得:AB2=22+22=8,
∴AA′=A′B=AB=2![]() ,A′M=
,A′M=![]() ,
,
∴C′M=![]() A′B=
A′B=![]() ;由勾股定理可求:AM=
;由勾股定理可求:AM=![]() ,
,
∴C′A=![]() ﹣
﹣![]() ,
,
故选:B.


科目:初中数学 来源: 题型:
【题目】如图,AB是⊙O的直径,AC,BC分別与⊙O交于点D,E,则下列说法一定正确的是( )
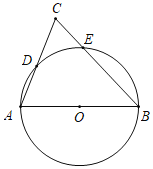
A.连接BD,可知BD是△ABC的中线B.连接AE,可知AE是△ABC的高线
C.连接DE,可知![]() D.连接DE,可知S△CDE:S△ABC=DE:AB
D.连接DE,可知S△CDE:S△ABC=DE:AB
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】小明在热气球A上看到正前方横跨河流两岸的大桥BC,并测得B、C两点的俯角分别为45°、35°.已知大桥BC与地面在同一水平面上,其长度为100m,求热气球离地面的高度.(结果保留整数)(参考数据:sin35°=0.57,cos35°=0.82,tan35°=0.70)
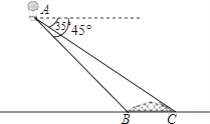
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某公司推销一种产品,公司付给推销员的月报酬有两种方案如图所示:方案一所示图形是顶点在原点的抛物线的一部分,方案二所示图形是射线.其中![]() (件)表示推销员推销产品的数量,
(件)表示推销员推销产品的数量,![]() (元)表示付给推销员的月报酬.
(元)表示付给推销员的月报酬.
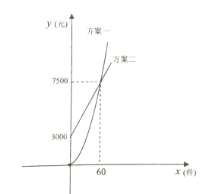
(1)分别求两种方案中![]() 关于
关于![]() 的函数关系式;
的函数关系式;
(2)当推销员推销产品的数量达到多少件时,两种方案月报酬差额将达到![]() 元?
元?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,△ABC内接于⊙O,∠B=600,CD是⊙O的直径,点P是CD延长线上的一点,且AP=AC.
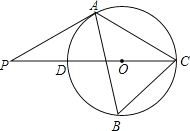
(1)求证:PA是⊙O的切线;
(2)若PD=![]() ,求⊙O的直径.
,求⊙O的直径.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知⊙O是△ABC的外接圆,AB是⊙O的直径,D是AB延长线上的一点,AE⊥CD交DC的延长线于E,交⊙O于G,CF⊥AB于F,点C是弧BG的中点.
(1)求证:DE是⊙O的切线;
(2)若AF,BF(AF>BF)是一元二次方程x2﹣8x+12=0的两根,求CE和AG的长.
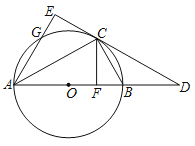
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】为弘扬中华民族传统文化,某市举办了中小学生“国学经典大赛”,比赛项目为:A.唐诗;B.宋词;C.论语;D.三字经.比赛形式分“单人组”和“双人组”.
(1)小华参加“单人组”,他从中随机抽取一个比赛项目,恰好抽中“论语”的概率是多少?
(2)小明和小红组成一个小组参加“双人组”比赛,比赛规则是:同一小组的两名队员的比赛项目不能相同,且每人只能随机抽取一次.则恰好小明抽中“唐诗”且小红抽中“宋词”的概率是多少?小明和小红都没有抽到“三字经”的概率是多少?请用画树状图或列表的方法进行说明.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】我国古代伟大的数学家刘徽将直角三角形分割成一个正方形和两对全等的直角三角形,得到一个恒等式.后人借助这种分割方法所得的图形证明了勾股定理.如图,若a=4,b=6,则该直角三角形的周长为( )
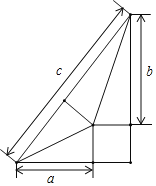
A.18B.20C.24D.26
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,某校教学楼AB的后面有一建筑物CD,当光线与地面的夹角是22时,
教学楼在建筑物的墙上留下高2m的影子CE;而当光线与地面的夹角是45时,教学楼顶A在地面上的影子F与墙角C有13m的距离(B、F、C在一条直线上).
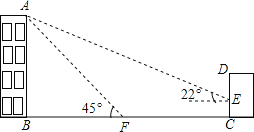
(1)求教学楼AB的高度;
(2)学校要在A、E之间挂一些彩旗,请你求出A、E之间的距离(结果保留整数).
(参考数据:sin22≈![]() ,cos22≈
,cos22≈![]() ,tan22≈
,tan22≈![]() )
)
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com