


 (-4,2)
(-4,2) 或t=2-
或t=2- ,又∵0<t≤2,∴t=2-
,又∵0<t≤2,∴t=2- .
. );
); 或t=4-
或t=4- ,又∵2<t≤4,∴t=4-
,又∵2<t≤4,∴t=4- .
. );
); ×4×(8-t)=16-2t,
×4×(8-t)=16-2t, ),(-4,2
),(-4,2 ),(-4,2).
),(-4,2).

科目:初中数学 来源:不详 题型:解答题
 ,AD‖BC,
,AD‖BC, ,
, ,
,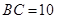 .
. 动点P、Q分别从A、C两点同时出发,点P以每秒1个单
动点P、Q分别从A、C两点同时出发,点P以每秒1个单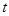 (0≤
(0≤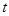 ≤5),
≤5),
查看答案和解析>>
科目:初中数学 来源:不详 题型:解答题

查看答案和解析>>
科目:初中数学 来源:不详 题型:单选题
 ,折叠后,点C落在AD边上的C1处,并且点B落在EC1边上的B1处.则BC的长为().
,折叠后,点C落在AD边上的C1处,并且点B落在EC1边上的B1处.则BC的长为().
A. | B.2 | C.3 | D. |
查看答案和解析>>
科目:初中数学 来源:不详 题型:解答题
 中,
中, 两点在边
两点在边 上,且四边形
上,且四边形 是平行四边形.
是平行四边形.
 与
与 有何等量关系?请说明理由;
有何等量关系?请说明理由; 时,求证:平行四边形
时,求证:平行四边形 是矩形.
是矩形.查看答案和解析>>
科目:初中数学 来源:不详 题型:填空题

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com