
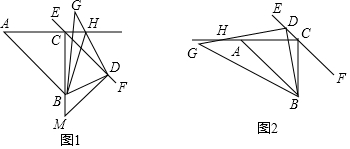
分析 (1)如图1中,作DN⊥EM于N,DP⊥AC于P.只要证明四边形PCND是矩形,△DPH≌△DNB,推出DH=BD,推出△BDH是等腰直角三角形,由此即可解决问题;
(2)如图2中,作DN⊥BC于N,DP⊥AC于P.只要证明四边形PCND是矩形,△DPH≌△DNB即可;
解答 (1)证明:如图1中,作DN⊥EM于N,DP⊥AC于P.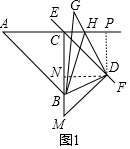
∵CA=CB,∠ACB=90°,
∴∠A=∠ABC=45°,
∵EF∥AB,
∴∠DCP=∠A=∠DCB=45°,
∵DN⊥EM于N,DP⊥AC于P,
∴DP=DN
∵∠PCN=∠DNC=∠DPC=90°,
∴四边形PCND是矩形,
∴∠PDN=∠BDH=90°,
∴∠PDH=∠BDN,
∴△DPH≌△DNB,
∴DH=BD,
∴△BDH是等腰直角三角形,
∴∠BHD=45°,
∵∠BHD=∠GBH+∠G,
∴∠GBH+∠G=45°,
∵DM⊥DC,
∴∠M=∠DCM=45°,
∴∠GBH+∠G=∠M.
(2)如图2中,作DN⊥BC于N,DP⊥AC于P.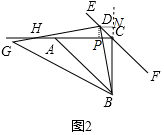
∵CA=CB,∠ACB=90°,
∴∠BAC=∠ABC=45°,
∵EF∥AB,
∴∠DCP=∠BAC=∠DCN=45°,
∵DN⊥EM于N,DP⊥AC于P,
∴DP=DN
∵∠PCN=∠DNC=∠DPC=90°,
∴四边形PCND是矩形,
∴∠PDN=∠BDH=90°,
∴∠PDH=∠BDN,
∴△DPH≌△DNB,
∴DH=BD,
点评 本题考查等腰直角三角形的性质、平行线的性质、全等三角形的判定和性质、矩形的判定和性质等知识,解题的关键是学会添加常用辅助线,构造全等三角形解决问题,属于中考考常考题型.


 金牌课堂练系列答案
金牌课堂练系列答案 三新快车金牌周周练系列答案
三新快车金牌周周练系列答案科目:初中数学 来源: 题型:解答题
 新学期伊始,学校联系厂家出售作业本,若学生在学校购买每个作业本1.5元,去校外的商店购买每个作业本2元.学校对学生一学期使用作业本的数量进行了调查,收集了30个学生一学期使用作业本的数据,整理绘制成如图的条形统计图:
新学期伊始,学校联系厂家出售作业本,若学生在学校购买每个作业本1.5元,去校外的商店购买每个作业本2元.学校对学生一学期使用作业本的数量进行了调查,收集了30个学生一学期使用作业本的数据,整理绘制成如图的条形统计图:查看答案和解析>>
科目:初中数学 来源: 题型:选择题
 如图,线段AB的坐标分别是A(2,4)、B(8,2),以原点O为位似中心,将线段AB缩小后得线段A′B′.若A点的对应点A′的坐标为(-1,-2),则点B的对应点B′的坐标是( )
如图,线段AB的坐标分别是A(2,4)、B(8,2),以原点O为位似中心,将线段AB缩小后得线段A′B′.若A点的对应点A′的坐标为(-1,-2),则点B的对应点B′的坐标是( )| A. | (-4,-1) | B. | (-1,-4) | C. | (5,-4) | D. | (-5,-4) |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
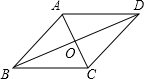 如图,四边形ABCD的对角线互相平分,若添加下列条件之一,不能使它变为菱形的条件是( )
如图,四边形ABCD的对角线互相平分,若添加下列条件之一,不能使它变为菱形的条件是( )| A. | AB=AD | B. | AC=BD | C. | BD平分∠ABC | D. | AC⊥BD |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com