
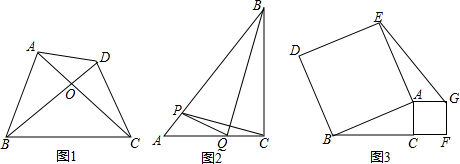
���� ��1�����ڶԽ����ഹֱ�������ı���ABCD������ɻ�Ϊ$\frac{1}{2}$AO•BD+$\frac{1}{2}$CO•BD�ĺͣ�
��2�����ڶԽ����ഹֱ���ɹ��ɶ����ֱ��ʾ��AB2��CD2��AD2��BC2��
��3���ٹ���P��PD��AC�ڵ�D�������PAD�ס�BAC������BP2+CQ2=PQ2+BC2�г�����t�ķ��̣�
������BE��CG��BG��CE��֤���ı���BCGE�Ǵ�ֱ�ı��Σ�Ȼ�����������ʡ�һ��Աߵ�ƽ���͵�����һ��Աߵ�ƽ���͡������ɵó�EG��BC��������ϵ��
��� �⣺��1�����ı���ABCD�ǡ���ֱ�ı��Ρ���
��AC��BD��
���ABD�����Ϊ��$\frac{1}{2}$AO•BD��
��CBD�����Ϊ��$\frac{1}{2}$CO•BD��
���ı���ABCD�������$\frac{1}{2}$AO•BD+$\frac{1}{2}$CO•BD
=$\frac{1}{2}$BD��AO+CO��
=$\frac{1}{2}$AC•BD
=$\frac{1}{2}$��8��7
=28��
�ʴ�Ϊ��28��
��2�����ı���ABCD�ǡ���ֱ�ı��Ρ���
��AC��BD��
�ɹ��ɶ�����֪��
AB2+CD2=��AO2+BO2��+��DO2+CO2����
AD2+BC2=��AO2+DO2��+��BO2+CO2����
��AB2+CD2=AD2+BC2�� ��3������ͼ2������P��PD��AC�ڵ�D��
��3������ͼ2������P��PD��AC�ڵ�D��
������֪��AP=5t��CQ=6t��
�ߡ�ACB=90�㣬
��AB=$\sqrt{{6}^{2}+{8}^{2}}$=10
��PD��BC��
���PAD�ס�BAC��
��$\frac{AD}{AC}=\frac{PD}{BC}$=$\frac{AP}{AB}$��
��$\frac{AD}{6}=\frac{PD}{8}=\frac{5t}{10}$��
��AD=3t��PD=4t��
��DQ=AC-AD-CQ=6-9t��
���ı���BCQP�ǡ���ֱ�ı��Ρ���
��BP2+CQ2=PQ2+BC2��
�ࣨ10-5t��2+��6t��2=��4t��2+��6-9t��2+82��
����t=$\frac{2}{9}$��t=0����ȥ����
�൱�ı���BCQP�ǡ���ֱ�ı��Ρ�ʱ��t��ֵΪ$\frac{2}{9}$��
��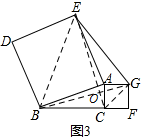 ��ͼ3������CG��BG��BE��CE��
��ͼ3������CG��BG��BE��CE��
CE��BG���ڵ�O
������֪��EA=BA��AC=AG
��EAB=��CAG=90��
���EAB+��BAC=��CAG+��BAC
���EAC=��BAG
�ڡ�EAC���BAG��$\left\{\begin{array}{l}{EA=BA}\\{��EAC=��BAG}\\{AC=AG}\end{array}\right.$��
���EAC�ա�BAG��SAS��
���CEA=��GBA
���EAB=��BOE=90��
���ı���BCGE�ǡ���ֱ�ı��Ρ�
��BC2+EG2=BE2+CG2��
��AB=3AC��
��EG2=$\frac{3}{2}$BC2��
���� ���⿼���¶��������⣬����Ĺؼ��Ƕ��¶�������⣬�漰�����ɶ�����ȫ�������ε��������ж������������ε��������ж���֪ʶ���ݣ���Ŀ����ӱ���ۺϣ���Ҫѧ�����¾�֪ʶ��ϵ������



| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
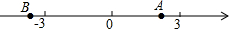 ��A��B�������ϵ�λ����ͼ��ʾ�����Ӧ�����ֱ���a��b���������½��ۣ��ף�b-a��0���ң�a+b��0������|a|��|b|������ab��0��������ȷ���ǣ�������
��A��B�������ϵ�λ����ͼ��ʾ�����Ӧ�����ֱ���a��b���������½��ۣ��ף�b-a��0���ң�a+b��0������|a|��|b|������ab��0��������ȷ���ǣ�������| A�� | �ס��� | B�� | ������ | C�� | �ס��� | D�� | �ҡ��� |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
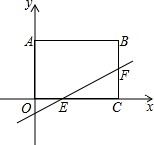 ��ͼ����ƽ��ֱ������ϵ�У�ֱ��y=$\frac{2}{3}$x-$\frac{2}{3}$�����ABCO�ı�OC��BC�ֱ��ڵ�E��F����֪OA=3��OC=4�����CEF�������3��
��ͼ����ƽ��ֱ������ϵ�У�ֱ��y=$\frac{2}{3}$x-$\frac{2}{3}$�����ABCO�ı�OC��BC�ֱ��ڵ�E��F����֪OA=3��OC=4�����CEF�������3���鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
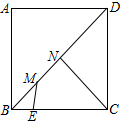 �ڱ߳�Ϊ5������ABCD�У���E��BC�ϣ���BE=2����M��N�ǶԽ���BD�����㣬��MN=$\sqrt{2}$�����ı���CEMN�ܳ���Сʱ����cos��BCN��ֵ$\frac{4}{5}$��
�ڱ߳�Ϊ5������ABCD�У���E��BC�ϣ���BE=2����M��N�ǶԽ���BD�����㣬��MN=$\sqrt{2}$�����ı���CEMN�ܳ���Сʱ����cos��BCN��ֵ$\frac{4}{5}$���鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | 4�� | B�� | 3�� | C�� | 2�� | D�� | 1�� |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com