
分析 (1)根据日利润=销售量×每件利润.每件利润为x-8元,销售量为100-10(x-10),据此得关系式.
(2)利用配方法即可解决问题.
(3)根据图象可知x=13时,y的值最大.
解答 解:(1)由题意得,y=(x-8)[100-10(x-10)]=-10x2+280x-1600,(10≤a<20),
(2)y=(x-8)[100-10(x-10)]=-10(x-14)2+360(10≤a<20),
∵a=-10<0
∴当x=14时,y有最大值360
答:他将售出价(x)定为14元时,才能使每天所赚的利润(y)最大,最大利润是360元.
(3)由图象可知x=13时,y的值最大,
答:将售价定为每件13元时,可以获最大利润.
点评 本题考查二次函数的应用,解题的关键是理解利润、销售量、每件利润之间的关系,学会构建二次函数解决在问题,属于中考常考题型.


科目:初中数学 来源: 题型:选择题
| A. | (x-1)(x-2)=x2-3x+2 | B. | x2-3x+2=(x-1)(x-2) | ||
| C. | x2-4x+4=x(x-4)+4 | D. | x2+y2=(x+y)(x-y)+2y2 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
| 星 期 | 一 | 二 | 三 | 四 | 五 |
| 市值涨跌 | +0.5 | +1.2 | -2.5 | +1.8 | -0.5 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
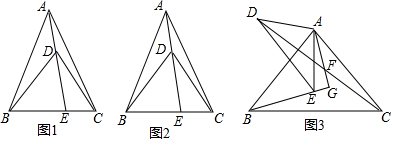
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com