
 如图,在宽为24m的马路两侧各竖立两根相同高度的灯杆AB、CD.当小明站在点N处时,在灯C的照射下小明的影长正好为NB,在灯A的照射下小明的影长NE=2m,试确定小明离路灯CD的距离.
如图,在宽为24m的马路两侧各竖立两根相同高度的灯杆AB、CD.当小明站在点N处时,在灯C的照射下小明的影长正好为NB,在灯A的照射下小明的影长NE=2m,试确定小明离路灯CD的距离. 分析 先根据题意得出△EMN∽△EAB,△BMN∽△BCD,再由相似三角形的对应边成比例即可得出结论.
解答 解:∵MN⊥BD,AB⊥BD,CD⊥BD,
∴△EMN∽△EAB,△BMN∽△BCD,
∴$\frac{NE}{BN+NE}$=$\frac{MN}{AB}$,$\frac{BN}{BD}$=$\frac{MN}{CD}$.
∵AB=CD,BD=24米,NE=2米,
∴$\frac{NE}{BN+NE}$=$\frac{BN}{BD}$,即$\frac{2}{BN+2}$=$\frac{BN}{24}$,解得BN=6米,
∴ND=24-6=18(米).
答:小明距路灯CD18米.
点评 本题考查的是相似三角形的应用,熟知相似三角形的对应边成比例是解答此题的关键.


 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:解答题
 中日钓鱼岛争端持续,我海监船加大钓鱼岛海域的巡航维权力度.如图,OA⊥OB,OA=36海里,OB=12海里,钓鱼岛位于O点,我国海监船在点B处发现有一不明国籍的渔船,自A点出发沿着AO方向匀速驶向钓鱼岛所在地点O,我国海监船立即从B处出发以相同的速度沿某直线去拦截这艘渔船,结果在点C处截住了渔船.
中日钓鱼岛争端持续,我海监船加大钓鱼岛海域的巡航维权力度.如图,OA⊥OB,OA=36海里,OB=12海里,钓鱼岛位于O点,我国海监船在点B处发现有一不明国籍的渔船,自A点出发沿着AO方向匀速驶向钓鱼岛所在地点O,我国海监船立即从B处出发以相同的速度沿某直线去拦截这艘渔船,结果在点C处截住了渔船.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
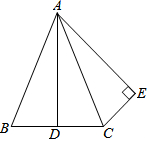 已知:如图,△ABC中,AB=AC,AD平分∠BAC,CE⊥AE于E,E在△ABC外,且CE=$\frac{1}{2}$BC.求证:∠ACE=∠B.
已知:如图,△ABC中,AB=AC,AD平分∠BAC,CE⊥AE于E,E在△ABC外,且CE=$\frac{1}{2}$BC.求证:∠ACE=∠B.查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com