
【题目】规定:[x]表示不大于x的最大整数,(x)表示不小于x的最小整数,[x)表示最接近x的整数(x≠n+0.5,n为整数),例如:[2.3]=2,(2.3)=3,[2.3)=2.则下列说法正确的是________.(写出所有正确说法的序号)
①当x=1.7时,[x]+(x)+[x)=6;
②当x=﹣2.1时,[x]+(x)+[x)=﹣7;
③方程4[x]+3(x)+[x)=11的解为1<x<1.5;
④当﹣1<x<1时,函数y=[x]+(x)+x的图象与正比例函数y=4x的图象有两个交点.
【答案】②③
【解析】
试题解析:①当x=1.7时,
[x]+(x)+[x)
=[1.7]+(1.7)+[1.7)=1+2+2=5,故①错误;
②当x=﹣2.1时,
[x]+(x)+[x)
=[﹣2.1]+(﹣2.1)+[﹣2.1)
=(﹣3)+(﹣2)+(﹣2)=﹣7,故②正确;
③当1<x<1.5时,
4[x]+3(x)+[x)
=4×1+3×2+1
=4+6+1
=11,故③正确;
④∵﹣1<x<1时,
∴当﹣1<x<﹣0.5时,y=[x]+(x)+x=﹣1+0+x=x﹣1,
当﹣0.5<x<0时,y=[x]+(x)+x=﹣1+0+x=x﹣1,
当x=0时,y=[x]+(x)+x=0+0+0=0,
当0<x<0.5时,y=[x]+(x)+x=0+1+x=x+1,
当0.5<x<1时,y=[x]+(x)+x=0+1+x=x+1,
∵y=4x,则x﹣1=4x时,得x=![]() ;x+1=4x时,得x=
;x+1=4x时,得x=![]() ;当x=0时,y=4x=0,
;当x=0时,y=4x=0,
∴当﹣1<x<1时,函数y=[x]+(x)+x的图象与正比例函数y=4x的图象有三个交点,故④错误,
故答案为②③.


科目:初中数学 来源: 题型:
【题目】已知:如图,在梯形ABCD中,AD∥BC,AB=DC,E是对角线AC上一点,且AC·CE=AD·BC.
(1)求证:∠DCA=∠EBC;
(2)延长BE交AD于F,求证:AB2=AF·AD.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在△ABC中,AB=AC,以AB为直径作⊙O交BC于点D.过点D作EF⊥AC,垂足为E,且交AB的延长线于点F.
(1)求证:EF是⊙O的切线;
(2)已知AB=4,AE=3.求BF的长.
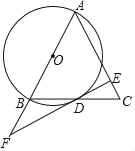
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系中,∠AOB=90°,∠OAB=30°,反比例函数y1=![]() 的图象经过点A,反比例函数y2=﹣
的图象经过点A,反比例函数y2=﹣![]() 的图象经过点B,则m的值是( )
的图象经过点B,则m的值是( )

A.m=3B.![]() C.
C.![]() D.
D.![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在平面直角坐标系![]() 中的点
中的点![]()
![]() ,将它的纵坐标
,将它的纵坐标![]() 与横坐标
与横坐标![]() 的比称为点
的比称为点![]() 的“湘一比”,记为
的“湘一比”,记为![]() ,如点
,如点![]() ,则
,则![]() .
.
(1)若![]() 在直线
在直线![]() 上,求点
上,求点![]() 的“湘一比”
的“湘一比”![]() 及直线
及直线![]() 与
与![]() 轴夹角的正切值;
轴夹角的正切值;
(2)已知点![]() 的“湘一比”
的“湘一比”![]() 为
为![]() ,且
,且![]() 在
在![]() 上,
上,![]() 的半径为
的半径为![]() ,若点
,若点![]() 在
在![]() 上,求
上,求![]() 的“湘一比”
的“湘一比”![]() 的取值范围;
的取值范围;
(3)设![]() 、
、![]() 为正整数,且
为正整数,且![]() ,对一切实数
,对一切实数![]() ,如果直线
,如果直线![]() 与二次函数
与二次函数![]() 交于
交于![]() 、
、![]() ,且
,且![]() ,求点
,求点![]() 的“湘一比”
的“湘一比”![]() 的值.
的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,小华在晚上由路灯A走向路灯B.当他走到点P时,发现他身后影子的顶部刚好接触到路灯A的底部;当他向前再步行12m到达点Q时,发现他身前影子的顶部刚好接触到路灯B的底部.已知小华的身高是1.6m,两个路灯的高度都是9.6m,且AP=QB.
(1)求两个路灯之间的距离;
(2)当小华走到路灯B的底部时,他在路灯A下的影长是多少?

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,防洪大堤的横截面ABGH是梯形,背水坡AB的坡度i=1:![]() (垂直高度AE与水平宽度BE的比),AB=20米,BC=30米,身高为1.7米的小明(AM=1.7米)站在大堤A点(M,A,E三点在同一条直线上),测得电线杆顶端D的仰角∠
(垂直高度AE与水平宽度BE的比),AB=20米,BC=30米,身高为1.7米的小明(AM=1.7米)站在大堤A点(M,A,E三点在同一条直线上),测得电线杆顶端D的仰角∠![]() =20°.
=20°.
(1)求∠ABC;
(2)求电线杆CD的高度.(结果精确到个位,参考数据sin20°≈0.3,cos20°≈0.9,tan20°≈0.4,![]() ≈1.7)
≈1.7)
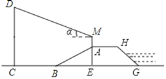
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系![]() 中,抛物线
中,抛物线![]() 与
与![]() 轴交于原点
轴交于原点![]() 和点
和点![]() ,点
,点![]() 在抛物线上.
在抛物线上.
(1)求抛物线的表达式,并写出它的对称轴;
(2)求![]() 的值;
的值;
(3)点![]() 在抛物线的对称轴上,如果
在抛物线的对称轴上,如果![]() ,求点
,求点![]() 的坐标.
的坐标.

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com