
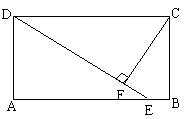
如图,四边形ABCD是矩形,E是AB上一点,且DE=AB,
过C作CF⊥DE,垂足为F.
(1)猜想:AD与CF的大小关系;
(2)请证明上面的结论.
 培优好卷单元加期末卷系列答案
培优好卷单元加期末卷系列答案科目:初中数学 来源: 题型:
我们把按照一定顺序排列的一列数称为数列,如1,3,9,19,33,…就是一个数列,如果一个数列从第二个数起,每一个数与它前一个数的差等于同一个常数,那么这个数列就叫做等差数列,这个常数叫做这个等差数列的公差.如2,4,6,8,10就是一个等差数列,它的公差为2.如果一个数列的后一个数与前一个数的差组成的新数列是等差数列,则称这个数列为二阶等差数列.例如数列1,3,9,19,33,…,它的后一个数与前一个数的差组成的新数列是2,6,10,14,…,这是一个公差为4的等差数列,所以,数列1,3,9,19,33,…是一个二阶等差数列.那么,请问二阶等差数列1,3,7,13,…的第五个数应是 _________ .
查看答案和解析>>
科目:初中数学 来源: 题型:
在一个不透明的袋子中装有4个除颜色外完全相同的小球,其中白球1个,黄球1个,红球2个,摸出一个球不放回,再摸出一个球,两次都摸到红球的概率是( )
A. 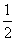 B.
B.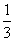 C.
C. 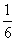 D.
D.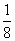
查看答案和解析>>
科目:初中数学 来源: 题型:
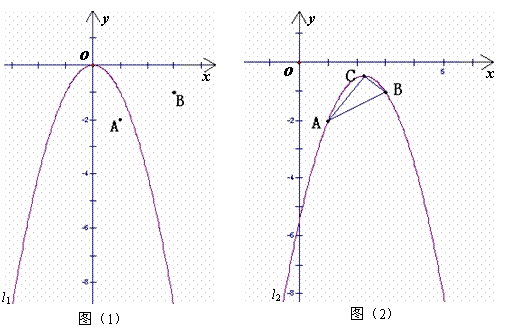
如图(1),在平面直角坐标系中,点A的坐标为(1,-2),点B的坐标为(3,-1),二次函数 的图象为
的图象为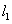 .
.
(1)平移抛物线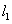 ,使平移后的抛物线过点A,但不过点B,写出平移后的抛物线的一个解析式(任写一个即可).
,使平移后的抛物线过点A,但不过点B,写出平移后的抛物线的一个解析式(任写一个即可).
(2)平移抛物线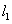 ,使平移后的抛物线过A、B两点,记抛物线为
,使平移后的抛物线过A、B两点,记抛物线为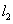 ,如图(2),求抛物线
,如图(2),求抛物线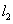 的函数解析式及顶点C的坐标.
的函数解析式及顶点C的坐标.
(3)设P为y轴上一点,且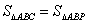 ,求点P的坐标.
,求点P的坐标.
(4)请在图(2)上用尺规作图的方式探究抛物线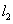 上是否存在点Q,使
上是否存在点Q,使 为等腰三角形. 若存在,请判断点Q共有几个可能的位置(保留作图痕迹);若不存在,请说明理由.
为等腰三角形. 若存在,请判断点Q共有几个可能的位置(保留作图痕迹);若不存在,请说明理由.

查看答案和解析>>
科目:初中数学 来源: 题型:
如图,在活动课上,小明和小红合作用一副三角板来测量学校旗杆高度.已知小明的眼睛与地面的距离(AB)是1.7m,他调整自己的位置,设法使得三角 板的一条直角边保持水平,且斜边与旗杆顶端M在同一条直线上,测得旗杆顶端M仰角为45°;小红的眼睛与地面的距离(CD)是1.5m,用同样的方法测得旗杆顶端M的仰角为30°.两人相距28米且位于旗杆两侧(点B、N、D在同一条直线上).求出旗杆MN的高度.(参考数据:
板的一条直角边保持水平,且斜边与旗杆顶端M在同一条直线上,测得旗杆顶端M仰角为45°;小红的眼睛与地面的距离(CD)是1.5m,用同样的方法测得旗杆顶端M的仰角为30°.两人相距28米且位于旗杆两侧(点B、N、D在同一条直线上).求出旗杆MN的高度.(参考数据: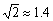 ,
,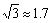 ,结果保留整数.)
,结果保留整数.)

查看答案和解析>>
科目:初中数学 来源: 题型:
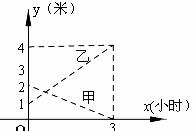
某企业有甲、乙两个长方体的蓄水池,将甲池中的水以每小时6立方米的速度注入乙池,甲、乙两个蓄水池中水的深度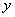 (米)与注水时间
(米)与注水时间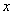 (时)之间的函数图象如图所示,注水时间为 小时甲、乙两个蓄水池的水的深度相同。
(时)之间的函数图象如图所示,注水时间为 小时甲、乙两个蓄水池的水的深度相同。
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com