
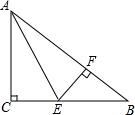
 如图,在Rt△ABC中,∠C=90°,∠A的平分线交BC于点E,EF⊥AB于点F,点F恰好是AB的一个三等分点(AF>BF).
如图,在Rt△ABC中,∠C=90°,∠A的平分线交BC于点E,EF⊥AB于点F,点F恰好是AB的一个三等分点(AF>BF).分析 (1)由角平分线的性质就可以得出CE=CF,在证明Rt△ACE≌Rt△AFE就可以得出结论;
(2)由点F是AB的一个三等分点(AF>BF)就可以得出AF=2BF,设BF=x,AF=2x,则AC=2x,AB=AF+BF=3x,由勾股定理就可以求出BC,表示出∠B的正切值,由三角函数值求出EF就可以求出结论.
解答 解:(1)∵∠C=90°
∴EC⊥AC.
∵AE平分∠BAC,EF⊥AB,
∴EC=EF.
在Rt△ACE和Rt△AFE中
$\left\{\begin{array}{l}{EC}={EF}\\{AE}={AE}\end{array}\right.$,
∴Rt△ACE≌Rt△AFE,
∴AC=AF;
(2)∵点F是AB的一个三等分点(AF>BF),设BF=x,AF=2x,则AC=2x,AB=AF+BF=3x.
在Rt△ACB中,由勾股定理,得
BC=$\sqrt{A{B^2}-A{C^2}}$=$\sqrt{{{(3x)}^2}-{{(2x)}^2}}$=$\sqrt{5}x$.
∵tan∠B=$\frac{AC}{BC}$=$\frac{2x}{{\sqrt{5}x}}=\frac{2}{{\sqrt{5}}}$,
∴在Rt△EFB中,EF=BF•tan∠B=$\frac{2x}{{\sqrt{5}}}$,
∴CE=EF=$\frac{2x}{{\sqrt{5}}}$.
∵tan∠CAE=$\frac{CE}{AC}$=$\frac{{\frac{2x}{{\sqrt{5}}}}}{2x}=\frac{{\sqrt{5}}}{5}$,
∴tan∠CAE=$\frac{{\sqrt{5}}}{5}$.
答:tan∠CAE的值为$\frac{\sqrt{5}}{5}$.
点评 本题考查了角平分线的性质的运用,全等三角形的判定及性质的运用,勾股定理的运用,三角函数值的运用,解答时证明三角形全等是关键.


 名校课堂系列答案
名校课堂系列答案科目:初中数学 来源: 题型:选择题
 如图,O是边长为a的正方形ABCD的中心,将一块半径足够长,圆心为直角的扇形纸板的圆心放在O点处,并将纸板的圆心绕O旋转,求正方形ABCD的边被纸板覆盖部分的面积为( )
如图,O是边长为a的正方形ABCD的中心,将一块半径足够长,圆心为直角的扇形纸板的圆心放在O点处,并将纸板的圆心绕O旋转,求正方形ABCD的边被纸板覆盖部分的面积为( )| A. | $\frac{1}{2}{a^2}$ | B. | $\frac{1}{3}{a^2}$ | C. | $\frac{1}{4}{a^2}$ | D. | 无法计算 |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 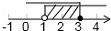 | B. | 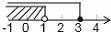 | C. |  | D. | 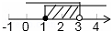 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
 如图,等腰直角△BCD中,BC=CD,E是边CD外的一点,且CE∥BD,BE=BD,则CE:BD的值$\frac{\sqrt{3}-1}{2}$.
如图,等腰直角△BCD中,BC=CD,E是边CD外的一点,且CE∥BD,BE=BD,则CE:BD的值$\frac{\sqrt{3}-1}{2}$.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com