练习册

  • 练习册
  • 试题
    精英家教网 > 初中数学 > 题目详情
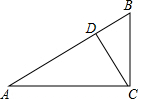
    15．如图，在Rt△ABC中，CD是斜边AB上的高，∠A≠45°，则下列比值中不等于sinA的是（　　）
    A．$\frac{CD}{AC}$B．$\frac{CB}{AB}$C．$\frac{BD}{CB}$D．$\frac{CD}{CB}$

    分析 根据锐角三角函数的定义解答即可．

    解答 解：∵在Rt△ABC中，CD是斜边AB上的高，
    ∴sinA=$\frac{CD}{AC}=\frac{CB}{AB}$，
    同时有，sinA=sin∠DCB=$\frac{DB}{CB}$．
    故选D．

    点评 本题考查了锐角三角函数的定义：在直角三角形中，锐角的正弦为对边比斜边，余弦为邻边比斜边，正切为对边比邻边．

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：初中数学 来源： 题型：解答题

    13．解方程：
    （1）$\frac{6}{3x}$=$\frac{1}{2x}$+2
    （2）$\frac{2x-3}{x+6}$=$\frac{1}{3}$．

    查看答案和解析>>

    科目：初中数学 来源：2016-2017学年江苏省苏州太仓市第二学期初一期中模拟数学试卷（解析版） 题型：单选题

    如果a＝(－0.1)0，b＝(－0.1)－1，c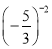＝，那么a，b，c的大小关系为( )

    A. a>b>c B. c>a>b C. c>b>a D. a>c>b

    查看答案和解析>>

    科目：初中数学 来源：2016-2017学年浙江省七年级3月月考数学试卷（解析版） 题型：解答题

    如图：在正方形网格中有一个△ABC，按要求进行下列作图（只借助于网格，需写出结论）：

    （1）过点B画出AC的平行线；

    （2）画出先将△ABC向右平移5格，得到△A’B’C’，再向上平移3格后的△A”B”C”；

    （3）对于（2）里面这两次平移的得到的图形能通过△ABC一次性平移得到吗？如果可以请你用合适的语言描述这个过程。

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

    11．观察思考
    某种在同一平面进行传动的机械装置如图1，图2是它的示意图．其工作原理是：滑块Q在平直滑道l上可以左右滑动，在Q滑动的过程中，连杆PQ也随之运动，并且PQ带动连杆OP绕固定点O摆动．在摆动过程中，两连杆的接点P在以OP为半径的⊙O上运动．数学兴趣小组为进一步研究其中所蕴含的数学知识，过点O作OH⊥l于点H，并测得OH=4分米，PQ=3分米，OP=2分米．

    解决问题
    （1）点Q与点O间的最小距离是4分米；点Q与点O间的最大距离是5分米；点Q在l上滑到最左端的位置与滑到最右端位置间的距离是6分米．
    （2）如图3，小明同学说：“当点Q滑动到点H的位置时，PQ与⊙O是相切的．”你认为他的判断对吗？为什么？
    （3）①小丽同学发现：“当点P运动到OH上时，点P到l的距离最小．”事实上，还存在着点P到l距离最大的位置，此时，点P到l的距离是3分米；
    ②当OP绕点O左右摆动时，所扫过的区域为扇形，求这个扇形面积最大时圆心角的度数．

    查看答案和解析>>

    科目：初中数学 来源：2016-2017学年浙江省七年级3月月考数学试卷（解析版） 题型：填空题

    如图，直线∥，∠3+∠4=35°，∠2=90°，则∠1=_______________。

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

    5．如图，平面直角坐标系中，Rt△ABC的三个顶点分别是A（-3，2），B（0，4），C（0，2）．
    （1）将△ABC以点C为旋转中心旋转180°，画出旋转后对应的△A1B1C；
    （2）平移△ABC，若点A的对应点A2的坐标为（0，-4），画出平移后对应的△A2B2C2；
    （3）若将△A1B1C绕某一点旋转可以得到△A2B2C2；请在坐标系中作出旋转中心S并写出旋转中心S的坐标：S（$\frac{3}{2}$，-1）
    （4）在x轴上有一点P，使得PA+PB的值最小，请作图标出P点并写出点P的坐标．P（-2，0）．

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

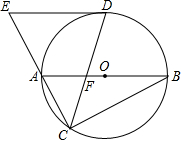    2．如图，⊙O是△ABC的外接圆，AB为⊙O的直径，∠ACB的平分线交⊙O于点D，交AB于点F；过D作⊙O的切线，交CA延长线于点E．
    （1）求证：AB∥DE；
    （2）写出AC、CD、BC之间的数量关系AC+BC=$\sqrt{2}$CD，并加以证明．
    （3）若tan∠B=$\frac{1}{2}$，DF=5$\sqrt{2}$，求DE的长．

    查看答案和解析>>

    科目：初中数学 来源： 题型：填空题

    3．如图，一次函数y=-$\frac{1}{2}$x+a（a＞0）的图象与坐标轴交于A，B两点，以坐标原点O为圆心，半径为2的⊙O与直线AB相离，则a的取值范围是a＞$\sqrt{5}$．

    查看答案和解析>>

    同步练习册答案