
 角形?若存在,求出点P的坐标;若不存在,说明其理由.
角形?若存在,求出点P的坐标;若不存在,说明其理由. 解:(1)AC∥BE;AC⊥OA,BE⊥OB,∠OAC=90°;OB=AB,OE=CE;
解:(1)AC∥BE;AC⊥OA,BE⊥OB,∠OAC=90°;OB=AB,OE=CE; AC,OA=2OB;∠BEO=∠ACO,∠CAO=∠EBO;
AC,OA=2OB;∠BEO=∠ACO,∠CAO=∠EBO;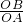 =
=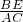 ;
; 的度数=
的度数= 的度数.
的度数. ,
, .
. .
. 代入原方程,得x2-(
代入原方程,得x2-( +1)x+
+1)x+ =0
=0 ,x2=1,
,x2=1,
 OB=
OB= ,OF=
,OF= .即B(
.即B(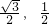 ).
). .
. ,y=
,y= x.
x.


 .∠GOE=∠BEO=30°.
.∠GOE=∠BEO=30°. ,OG=
,OG= ,OH=
,OH= .G(-
.G(- ,
, ).
). x+2.
x+2.
 (即为E点,舍去)
(即为E点,舍去)
 ,-
,- )或(-
)或(- ,
,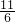 ).
).

科目:初中数学 来源: 题型:
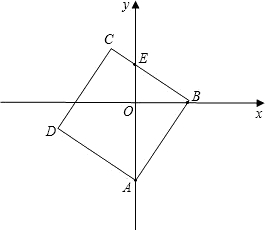 BCD某一边的交点,设点B的坐标为(t,0),线段OE的长度为m.
BCD某一边的交点,设点B的坐标为(t,0),线段OE的长度为m.查看答案和解析>>
科目:初中数学 来源: 题型:
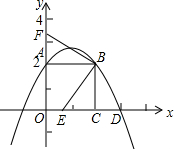 如图,已知正方形OABC的边OA在y轴的正半轴上,OC在x轴的正半轴上,OA=AB=2,抛物线y=-
如图,已知正方形OABC的边OA在y轴的正半轴上,OC在x轴的正半轴上,OA=AB=2,抛物线y=-| 2 | 3 |
查看答案和解析>>
科目:初中数学 来源: 题型:
 ,并且OC>OE.
,并且OC>OE.查看答案和解析>>
科目:初中数学 来源: 题型:
| 1 |
| 2 |
| k |
| x |
| 5 |
| 5 |

查看答案和解析>>
科目:初中数学 来源:三点一测丛书九年级数学上 题型:044
已知,如图,![]() 小于半圆周,它所在的圆的圆心为O,半径为13,弦AB的长为24;C是弦AB上的一个动点(异于A、B),过C作AB的垂线交
小于半圆周,它所在的圆的圆心为O,半径为13,弦AB的长为24;C是弦AB上的一个动点(异于A、B),过C作AB的垂线交![]() 于点P,以PC为直径的圆交AP于点D;E为AP的中点,连结OE.
于点P,以PC为直径的圆交AP于点D;E为AP的中点,连结OE.

(1)当点D、E不重合时,如图(1),求证OE∥CD;
(2)当点C是弦AB的中点时,如图(2),求PD的长;
(3)当点D、E重合时,请你推断∠PAB的大小为多少度(只需给出结论,不必给出证明).
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com